
Here we will examine the graphs of y=a sin(bx + c) for different values of a, b, and c.
Let us first look at the effects of changing a while b and c remain constant.
![]()
![]()
![]()
![]()
![]()
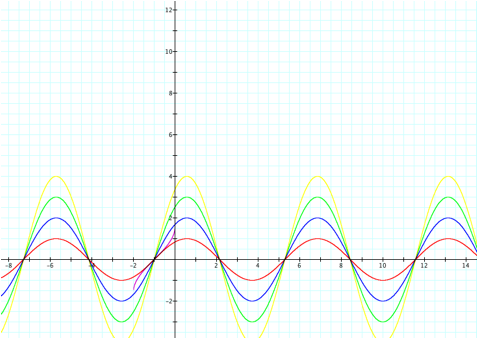
We can see that the amplitudes are changing, if we look more
closely at the graphs of y= 1 sin (1x + 1) and 4 sin (1x + 1) we will observe the following.
![]()
![]()
Notice that the amplitude is
greater with the larger value of a, and corresponds with its value on the
y-axis. So, what might we expect
to see with negative values for a?
![]()
![]()
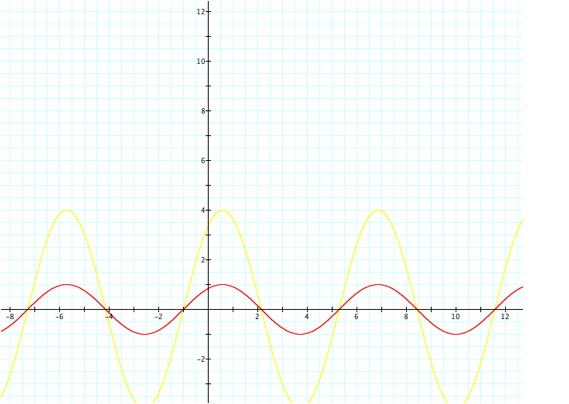
For negative values of a, the
amplitude is negative and still corresponds with its value on the y-axis. From these observations we can conclude
that the change in a determines the type of vertical
expansion of the function.
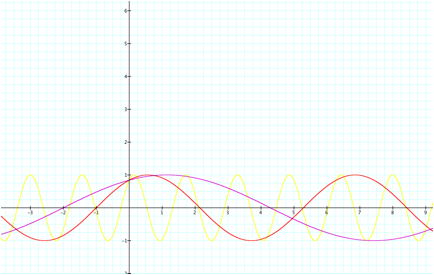
Now let us observe the effects of changes in b on the
graph.
![]()
![]()
![]()
![]()
![]()
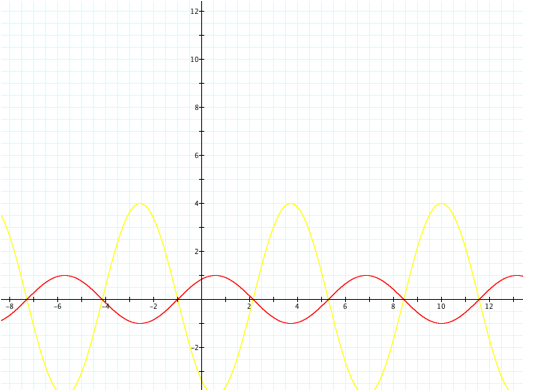
Notice the graphs have
different periods. If we look at
the graphs when a and c are constant and b=1, 4, and ½ we can take a closer look at how the periods are changing with
the change in b.
![]()
![]()
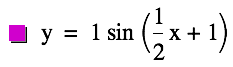
The change in the period can
be determined with the formula ![]() , therefore we can see why 0 < b > 1 would yield a horizontal
expansion (shown when b = ½) and b > 1 would yield a horizontal compression.
, therefore we can see why 0 < b > 1 would yield a horizontal
expansion (shown when b = ½) and b > 1 would yield a horizontal compression.
Lastly, letŐs observe changes
in c.
![]()
![]()
![]()
![]()
![]()
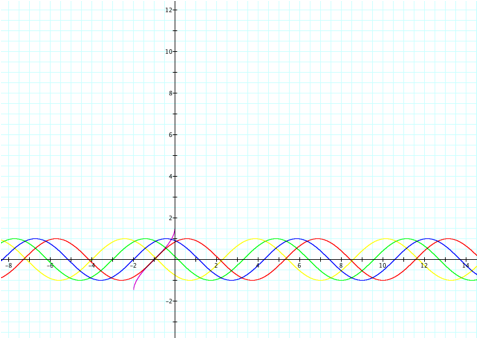
Here we can see that the
graphs are translated horizontally.
If we take a closer look
![]()
![]()
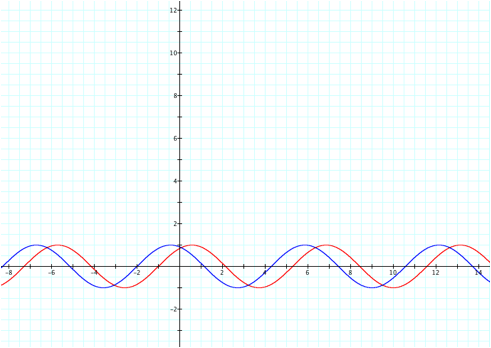
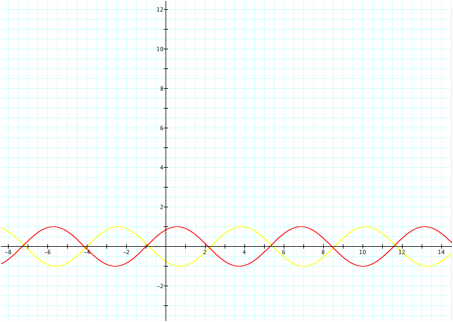
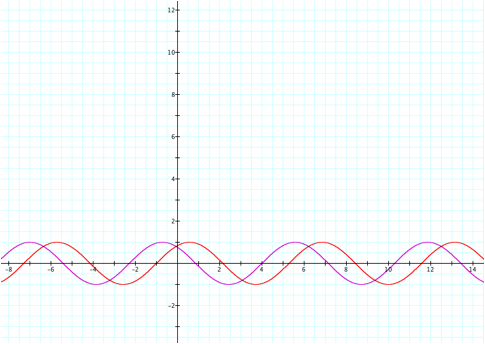
We can see that the graph
shifts to the left for c>0,
![]()
![]()
![]()
![]()
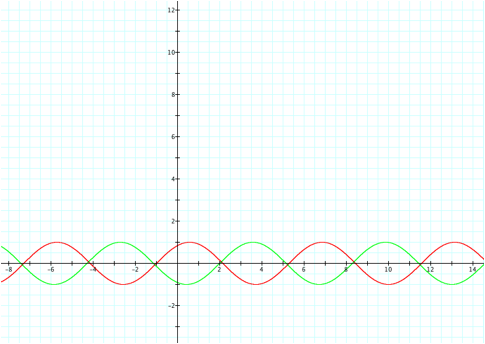
and shifts to the right for c<0.
![]()
![]()
Based on the observations we
have made what do you think would happen if we changed the original equation to y=a sin(bx + c) +
d. We have already demonstrated
changes in amplitude, period, and horizontal expansion/compression, so we could
logically assume that changes in d will result in a vertical
expansion/compression.
LetŐs see.
![]()
![]()
![]()
![]()
![]()
![]()
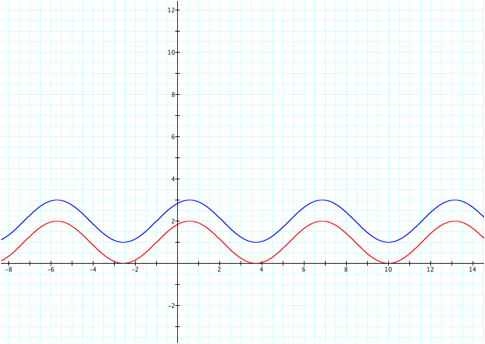
![]()
![]()
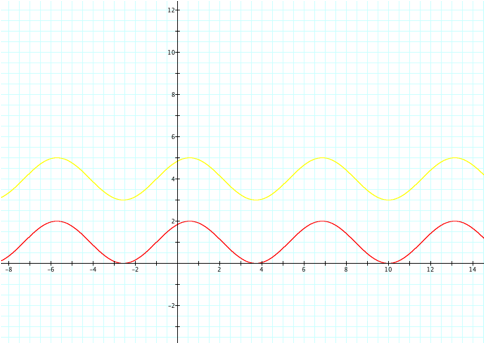
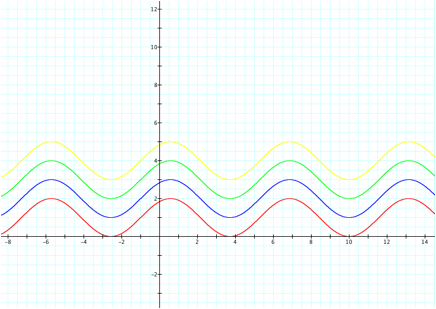
We can see that when d>0 the graph
shifts up,
![]()
![]()
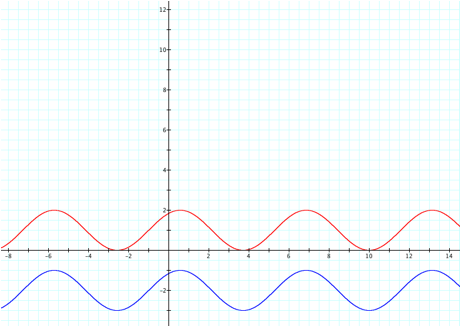
and for values of d<0 the graph shifts down.
So for
y=a
sin(bx + c) + d
|a| = amplitude
![]() = phase
shift
= phase
shift
c
= horizontal expansion/compression
d
= vertical expansion/compression