Let’s begin this investigation by looking at several graphs of y = aX², with varying values of a. For this exploration we will look specifically at a=1,,5,-, and -5. The graph of a=1 will be used as a control graph to compare with the graphs of the other values of a. We’ll start by looking at all of the graphs.

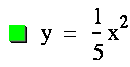
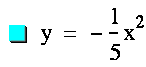
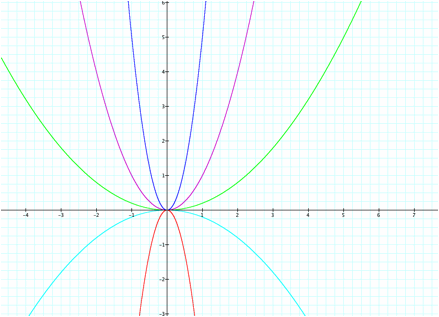
If we look specifically at the graphs of y= 5x² and y=-5x² as compared to y= x² we can readily see the distinction between y= 5x² and y=-5x². The graph of y=5x² opens concave upwards while the graph of y=-5x² opens concave downwards or we can simply say that y=-5x² is y= 5x² reflected over the x-axis.

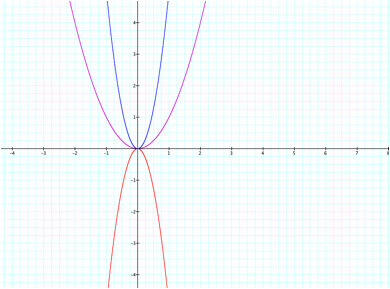
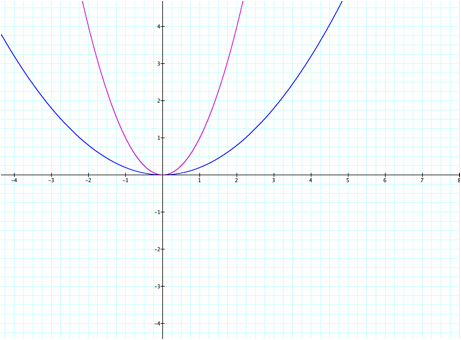
We must also compare these graphs to the graph of y= x². Here we can see that the graphs of y= 5x² and y=-5x² are more narrow than the graph of y= x². This is a dilation, more specifically a vertical expansion of y= x².

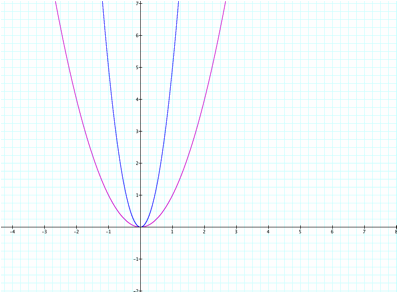
Notice that the graph becomes steeper (more narrow) when a is increased to 5. As a increases the graph continues to become steeper, hence the term vertical expansion.

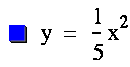
Here we see the graph becomes wider for 0 < a <1. This is called a vertical compression because the graph is wider and shorter.

Parabola Activity

Return