Tree Growth | Home

 

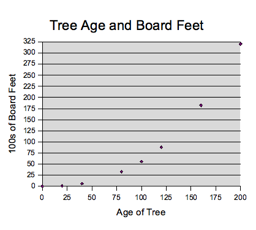
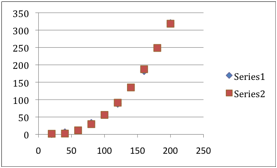
The first task of this exploration was to plot the given data.  From the figure below, it looked like the curve is quadratic, cubic (or perhaps exponential).  It seemed plausible that the number of board feet would grow in a quadratic manner (assuming a fixed height was usable lumber) since the diameter of the tree would grow linearly with respect to time, so the area of the cross-section would grow quadratically with respect to time.  However, this model doesn't seem to take into account the growth in the tree's height, so it may be a case of a cubic (or exponential) relationship approximated by a quadratic function.

 

 

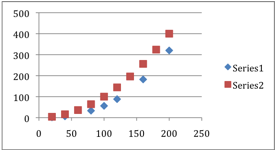
The first model was just 10% of the tree's age, squared.  The error for this model is quite high, and the discrepancy between the model and the data is quite obvious when they are plotted together.

 

Age of Tree	100s of Board Feet	Model	Squared Error
		(x*0.1)^2
20	1	4	9
40	6	16	100
60		36
80	33	64	961
100	56	100	1936
120	88	144	3136
140		196
160	182	256	5476
180		324
200	320	400	6400
		TOTAL:	18018

 

 

 

 

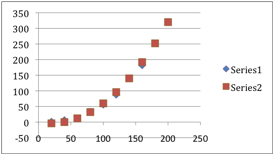
Subtracting 40% of the tree's age improved the model by a significant amount, but my goal was to get the total squared error under 100.

 

Age of Tree	100s of Board Feet	Model	Squared Error
		(x*0.1)^2-(x*0.4)
20	1	-4	25
40	6	0	36
60		12
80	33	32	1
100	56	60	16
120	88	96	64
140		140
160	182	192	100
180		252
200	320	320	0
		TOTAL:	242

 

 

The next improvement of the model was to add a linear term. I noticed that many of the expected values were below what was observed.

 

Age of Tree	100s of Board Feet	Model	Squared Error
		(x*0.1)^2-(x*0.5)+10
20	1	4	9
40	6	6	0
60		16
80	33	34	1
100	56	60	16
120	88	94	36
140		136
160	182	186	16
180		244
200	320	310	100
		TOTAL:	178

 

 

 

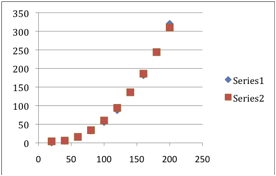
Although the model was significantly improved, I thought I could do better.  The last step was to fine tune each parameter by trial and error, beginning with the coefficient of the quadratic term and finishing with the linear term.

 

Age of Tree	100s of Board Feet	Model	Squared Error
		(x*0.104)^2-(x*0.62)+9.8
20	1	1.7264	0.52765696
40	6	2.3056	13.64859136
60		11.5376
80	33	29.4224	12.79922176
100	56	55.96	0.0016
120	88	91.1504	9.92502016
140		134.9936
160	182	187.4896	30.13570816
180		248.6384
200	320	318.44	2.4336
		TOTAL:	69.4713984

 

 

The last model achieved my goal, having a total squared error of less than 100.  Since the model's purpose is to provide approximations of the number of board feet at 60, 140, and 180 years I would argue that the model's estimates for each of these may be revised.  The model's values are below those observed at 40 and 80 years and so it is sensible to expect its value at 60 years will be also be low.  Similarly, the model's values for 120 and 160 years are both high, so it is likely that its value for 140 years will likewise be high.  Since the model's value is low for 200 years, its prediction for 180 may be high or low of the actual value.