Areas and Orthocenters | Home

 

In this assignment I explore the figure:

 

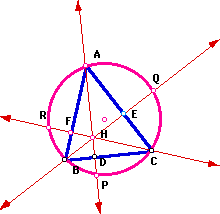
The circle is the circumcircle of the acute triangle ABC with orthocenter H.  The segments AD, BE, and CF are its three altitudes. The points P, Q, and R are the intersection of the altitudes with the circumcenter.

 

I compute the value of two sums,

 

 and ,

 

and prove these results.

 

First recall that the area of �ABC is found by one-half the product of the length of one side and the length of the altitude of that side. Next, observe that the area of �ABC can also be found by summing the areas of the component triangles �BCH, �ACH, and �ABH. Each of these triangles has a base that is also a side of the �ABC. It follows, that each ratio in the first sum above is equal to the ratio of the area of one component triangle and the area of the largest triangle:

 

 

Thus, the first sum is 1.

 

To find the value of the second sum, we write each numerator as the difference of two values:

 

 

It follows that the second sum is three more than the additive inverse of the first sum. Thus, the second sum is 2.