Assignment VI: Triangle and Medians
by
Rui Kang
Our tasks in this investigation are:
Construct a triangle and its medians.
Construct a second triangle with the three sides having the lengths of the three medians from your first triangle.
Find some relationship between the two triangles.
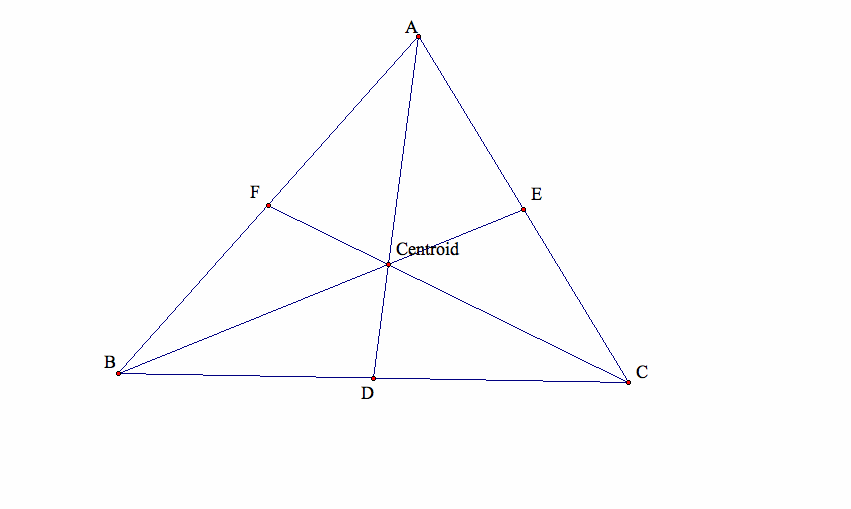
First, we draw a triangle ABC and then its three medians, let's call them AD, BE, CF.
We know from Assignment 4 that the three medians intersect at one point, which happens to be the centroid of the triangle ABC.
Second, let's construct a second triangle with the three sides having the lengths of the three medians from our first triangle.
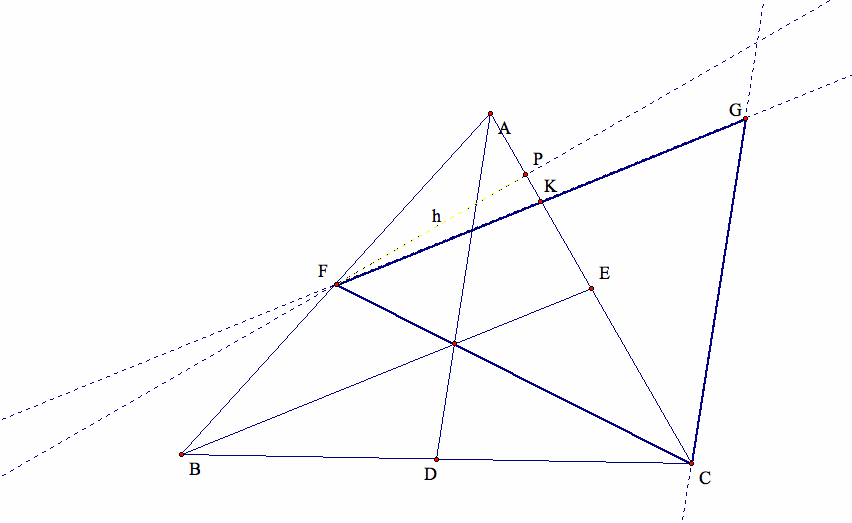
These are the steps by which this second triangle is created:
(1) First, we decide that we want to keep one of the medians to make this second triangle somewhat attached to the first triangle.
And hopefully this will make our investigation of the relations between the first and the second triangles easier. So we decide to keep the median CF.
(2) Second, we draw a line passing through F that is parallel to BE, let's call this line 
.
In addition, we mark a vector from B to E and then translate the point F along the line to a point G such that |FG|=|BE|.
(3) Finally, we draw another line passing through C that is parallel to AD, let's call this line 
.
Similar to (2), we mark a vector from D to A and then translate the point C along the line , to a point G' such that |CG'|=|AD|.
Note that G and G' are concurrent, so we get a second trangle CFG with three sides having the lengths of the three medians from our first triangle ABC.
In particular, |CF|=|CF|, |BE|=|FG|, and |AD|=|CG|.
Now we have finished our construction of the second triangle.
Before we go further, we want to start our proof with a simple fact that will make our later tasks much easier.
In particular, we claim that a median of a triangle divides the traingle into two smaller triangles with equal area.
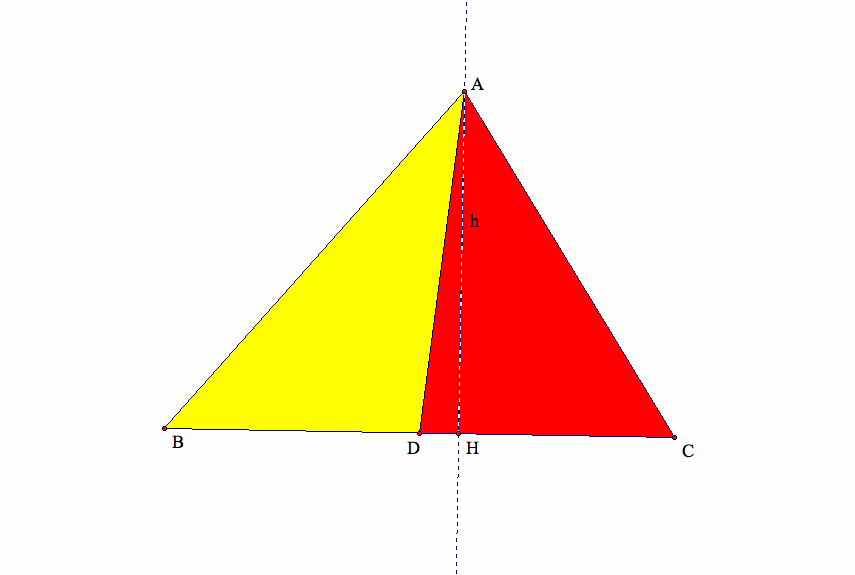
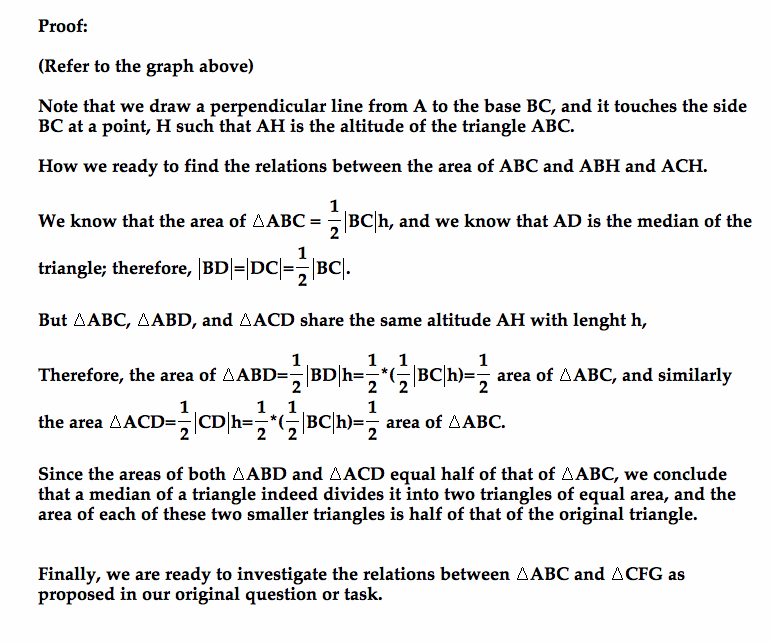
Let's observe the picture one more time:
