Assignment VII: Tangent Circles
by
Rui Kang
In this investigation, we explore the various cases of the following problem:
Given two circles and a point on one of the circles.
Construct a circle tangent to the two circles with one point of tangency being the designated point.
Base case:
Given two circles, one is nested in the other. We construct a desired circle that is tangent to both of the original circles.
Let us look at two possibilities:
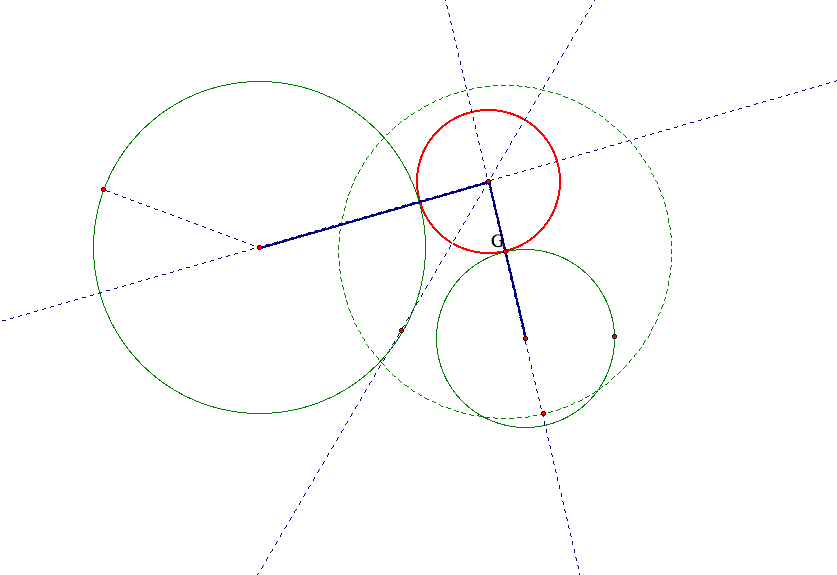
In the above graph, note that the tangent circle (in red) is inside the larger given circle and outside the smaller given circle.
We later call this scenario sub-case 1.
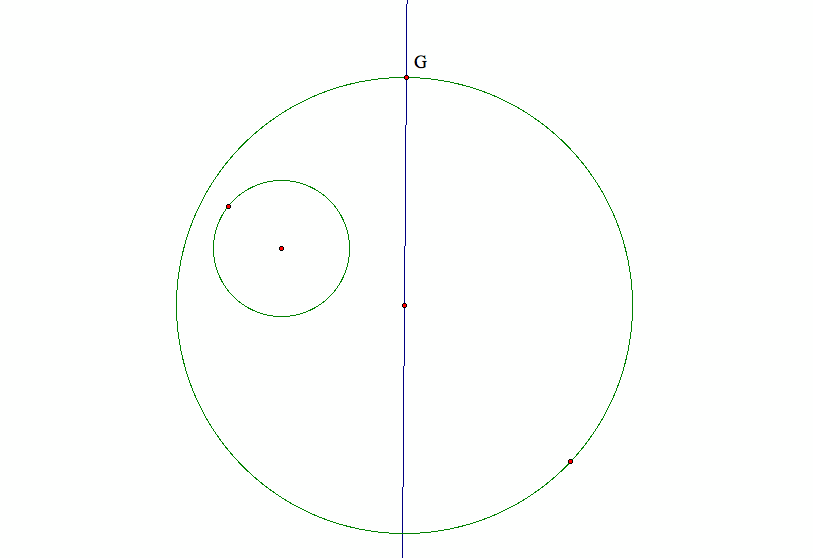
In the above graph, note that the tangent circle (in red) is inside the larger given circle,
and the smaller given circle is inside the tangent circle.
We later call this scenario sub-case 2.
Next we will trace the construction process of both Graph 1 & 2.
By doing so, we will gain insights about this particular case, other related cases of this problem, and
a considerable array of other problems and investigations related to the set of circles tangent to two given circles.
Construct sub-case 1:
The center of the desired circle will lie along a line from the center of the given circle with the specified point (G).
So far, we have found one locus of the center of the tangent circle,
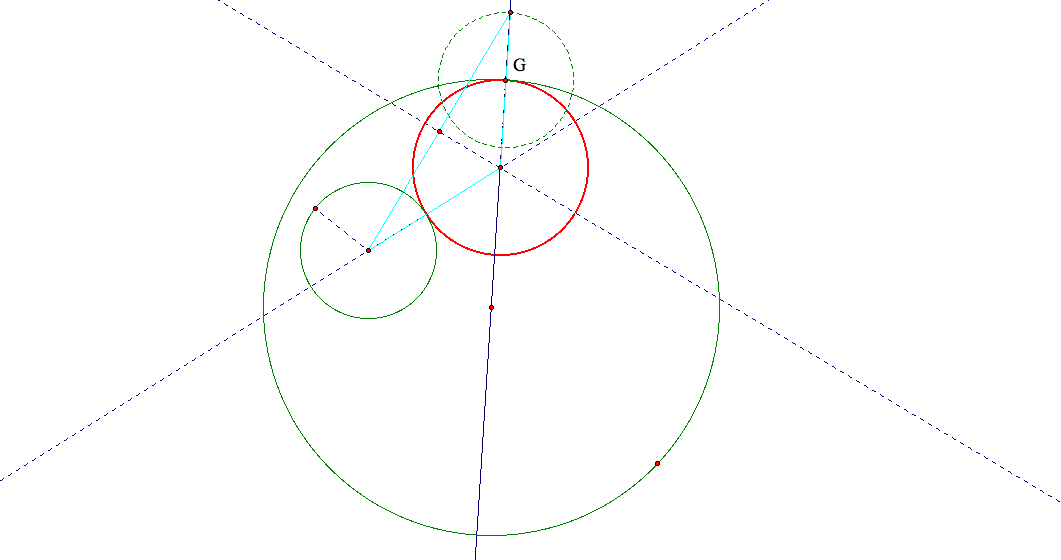
We need to find another locus for the center of the tangent circle. Consider if the problem is solved, we would have this configuration:
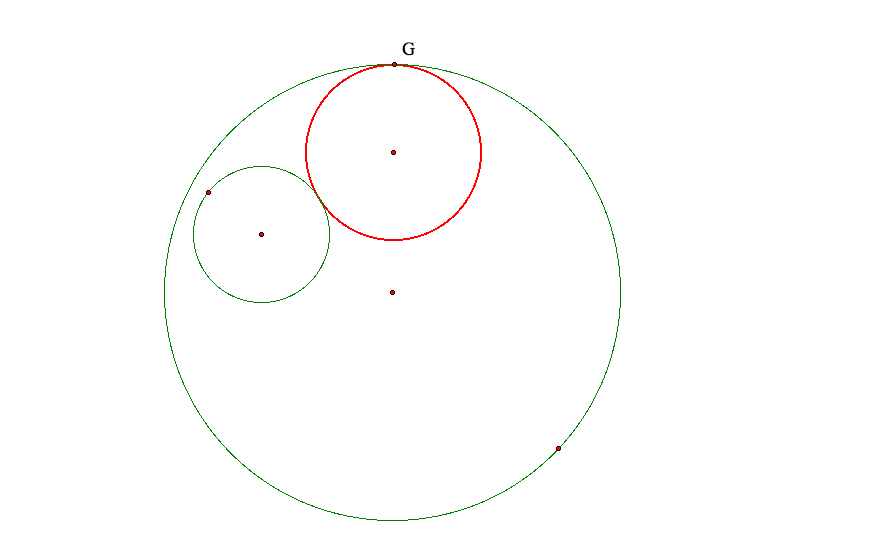
Then if we added the lines through the centers. We would have this situation:
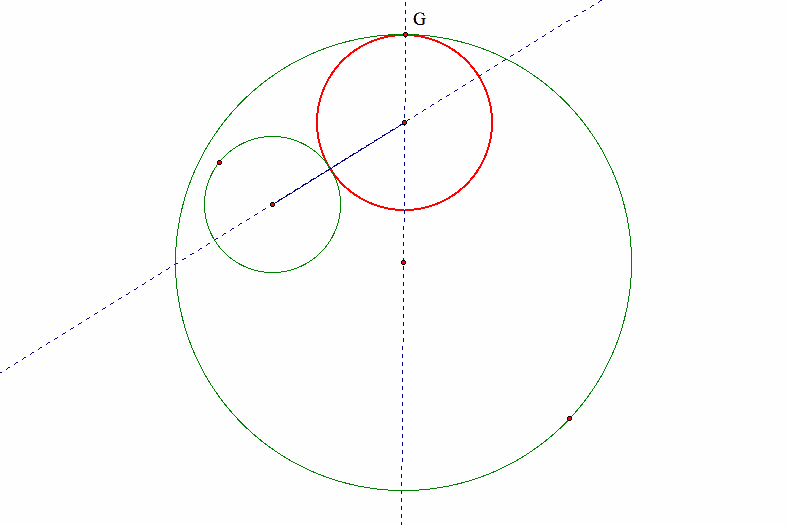
Now consider the segment from the center of the desired circle to the center of the second given circle.
This segment is always of the length the sum of the radius of the desired circle plus the radius of the given circle that did not have the specified point.
The same distance can be laid off along the line through the given point from the center of the desired circle,
by constructing an additional circle of the same radius as the second given circle.
The center of this additional circle is located at the designated tangent point, as shown below:
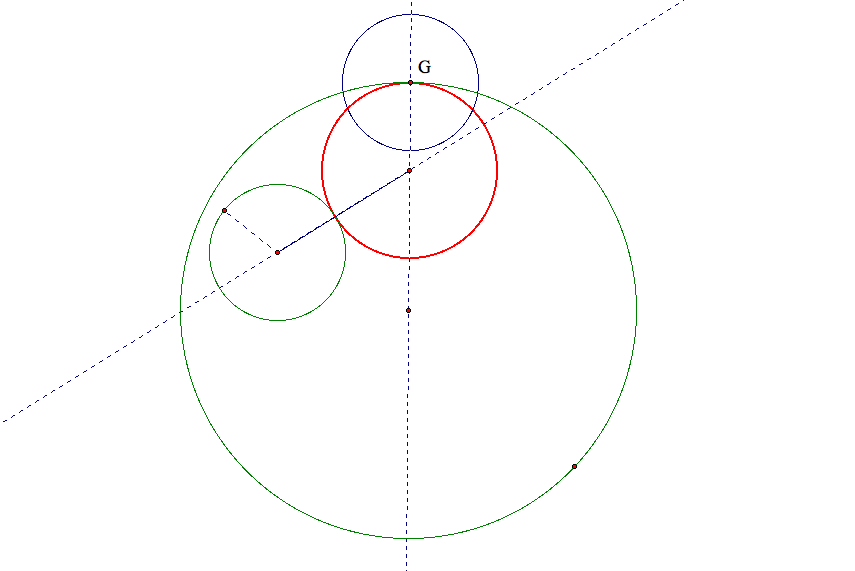
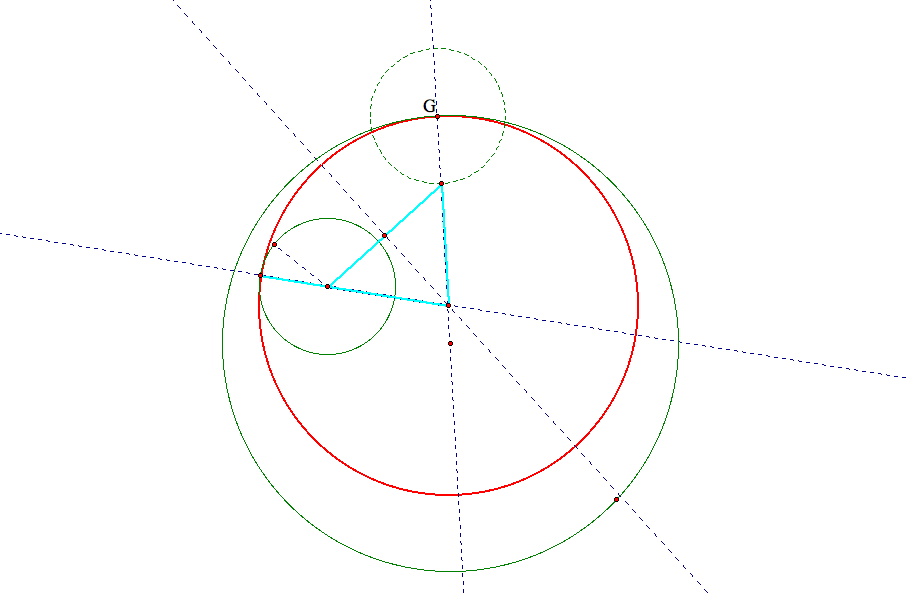
Now an isosceles triangle is formed, like so,
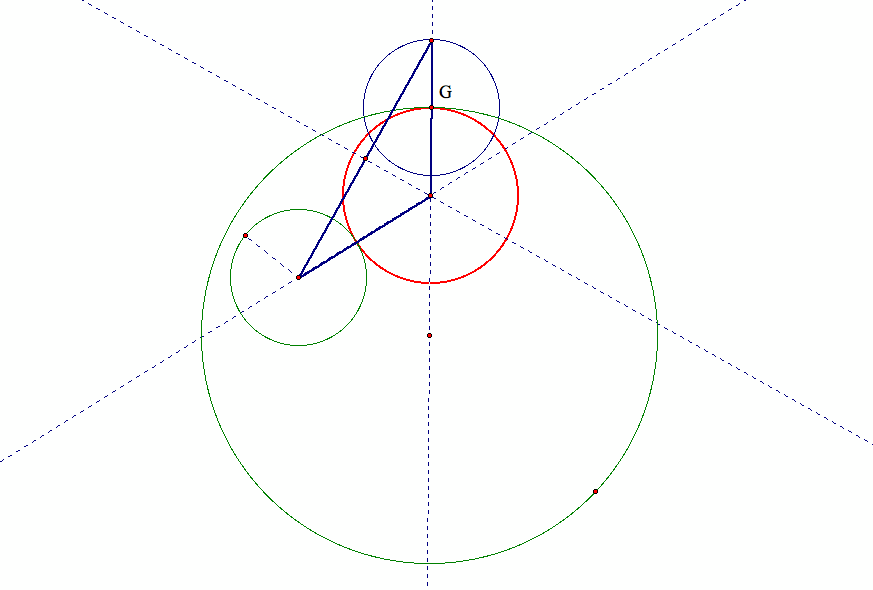
And therefore the center of the desired tangent circle lies along the perpendicular bisector of the base of the constructed isosceles triangle (in dark blue),
and now we have a construction of the desired circle. That is,
(1) construct a line through the center of the circle with the designated point of tangency,
(2) and then construct a circle of the same radius of the second given circle with the designated point as center,
(3) the intersection of the line and this additional circle will allow construction of the base of an isosceles triangle,
(4) draw the perpendicular bisector of the base of the isosceles triangle which intersects the line in (1) at a point,
and this point happens to be the center of the desired circle.
The radius of the desired circle is simply from this point to the designated point of tangency.
The construction of sub-case 2 is very similar to that of sub-case :

The center of the desired circle will lie along a line from the center of the given circle with the specified point (G).
So far, we have found one locus of the center of the tangent circle.
We need to find another locus for the center of the tangent circle. Consider if the problem is solved, we would have this configuration:
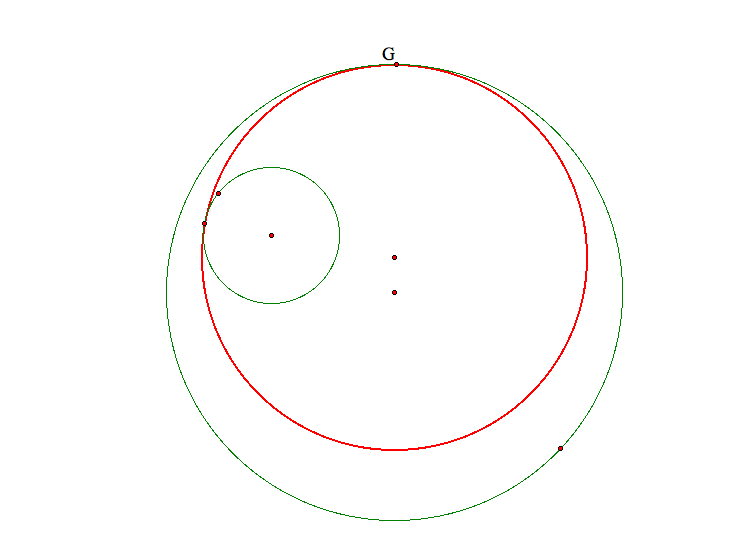
Then if we added the lines through the centers. We would have this situation:
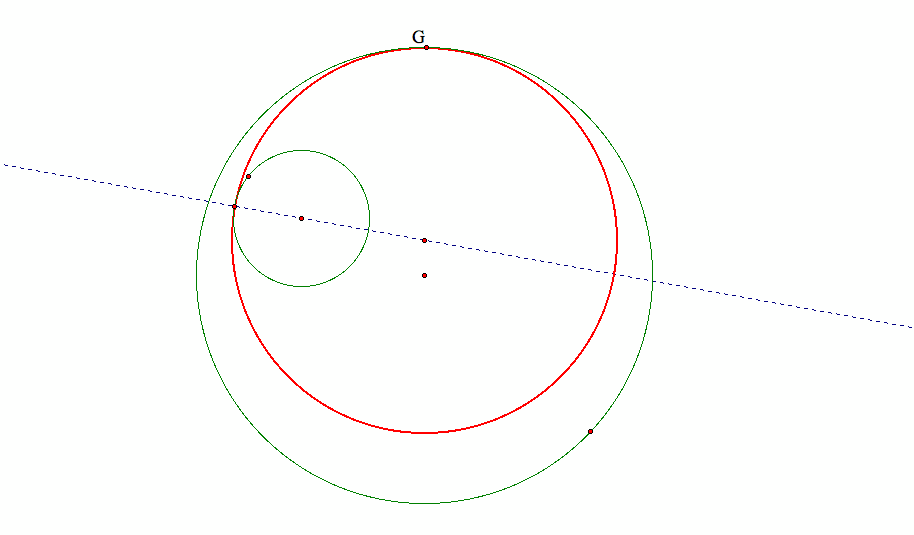
Now consider the segment from the center of the desired circle to the center of the second given circle.
This segment is always of the length the difference between the radius of the desired circle and the radius of the given circle that did not have the specified point.
The same distance can be laid off along the line through the given point from the center of the desired circle,
by constructing an additional circle of the same radius as the second given cricle.
The center of this additional circle is located at the designated tangent point, as shown below:
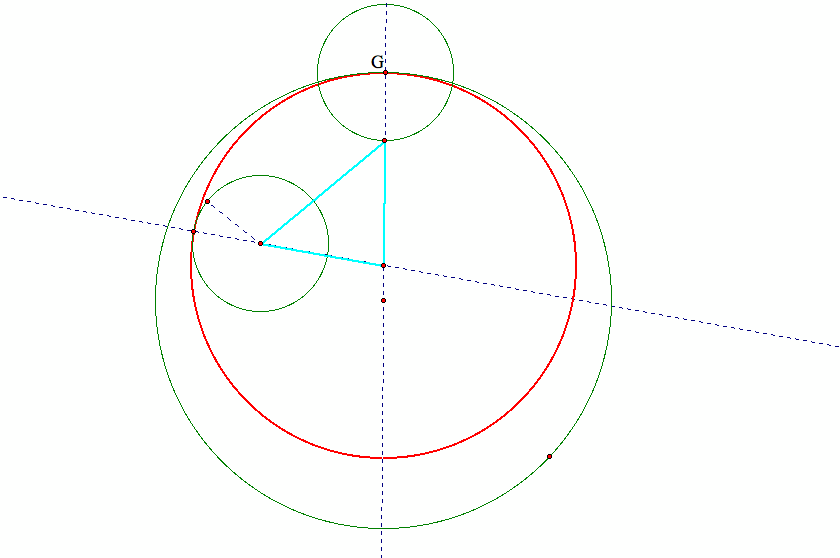
Now an isosceles triangle is formed (in light blue),
and therefore the center of the desired tangent circle lies along the perpendicular besector of the base of this isoscles traingle,
and now we have a construction of the desired circle. That is,
(1) construct a line through the center of the circle with the designated point of tangency,
(2) and then construct a circle of the same radius of the second given circle with the designated point as center,
(3) the intersection of the line and this additional circle will allow construction of the base of an isosceles triangle,
(4) draw the perpendicular bisector of the base of the isosceles triangle which intersects the line in (1) at a point,
and this point happens to be the center of the desired circle.
The radius of the desired circle is simply from this point to the designated point of tangency.
(A side note: the only difference between sub-case 1 and sub-case 2 is in step (3):
In sub-case 1 we choose the intersection of the additional circle and the line in (1) that is beyond the first given circle
(farther from the center of the first given circle).
We construct the base of the isosceles triangle from this intersection to the center of the second given circle.
In sub-case 2, however, we choose the intersection of the additional circle and the line in (1) that is inside of the first given circle
(closer to the center of the first given circle).
We construct the base of the isosceles triangle from this intersection to the center of the second given circle.)
Now we are ready to examine the locus of the center of all such circles tangent to the two given circles.
With GSP, we can animate the specified point of tangency around the circle and trace the locus of the center of the tangent circle as follows:
If the center of the tangent circle is connected by the segments to the centers of the two given circles,
it is immediate that the sum of the segments is the same as the sum of the radii of the two given circles.
To see this is true for sub-case 1, observe the following graph:
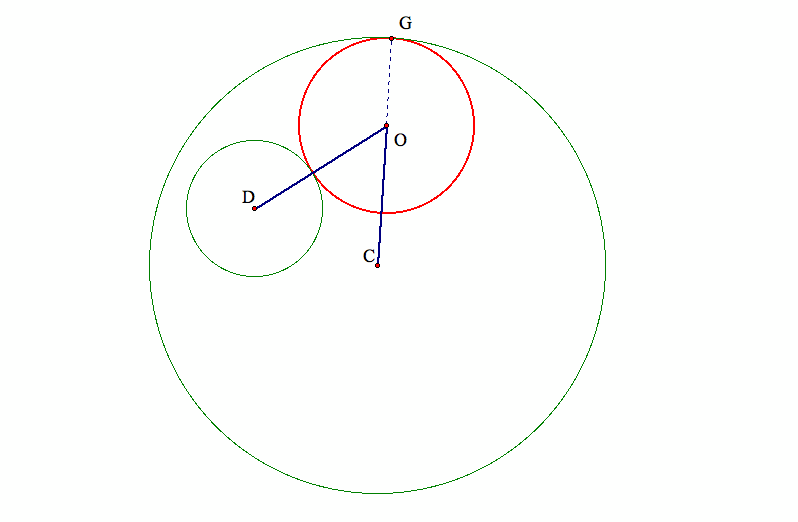
Let's call the radius of the larger given circle R, that of the smaller given circle r, and that of the tangent cricle r1,
we need to show the sum of the two thick blue segments is the sum of R+r.
But |OD|=r+r1, |OC|=R-r1
Therefore, |OD|+|OC|=r+r1+R-r1=r+R.
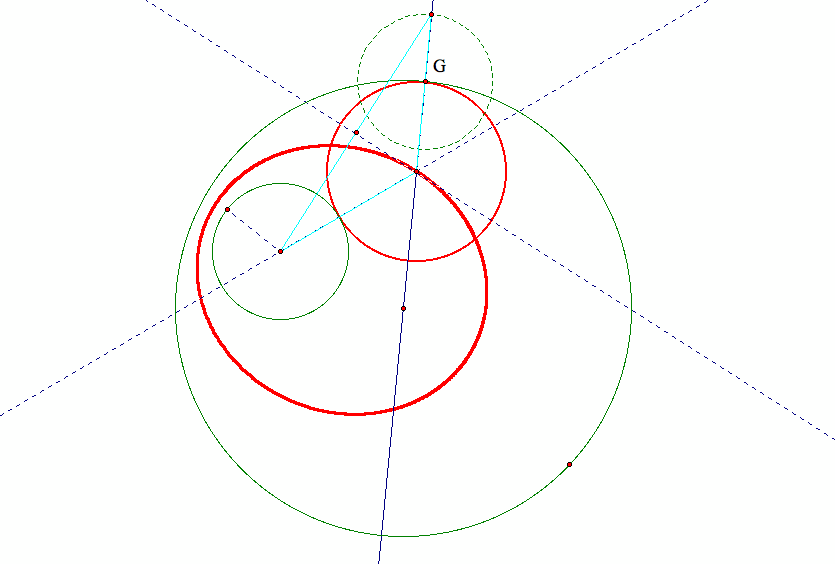
The sum of |OD| + |OC| is a constant and therefore, we expect that the locus of the centers of the tangent circles is an ellipse
with foci at the centers of the given circles.
Use the trace function of GSP, we have confirmed that the centers of the tangent circles is an ellipse for sub-case 1:
Now let's use the same method to examine sub-case 2 and the locus of the center of all such circles tangent to the two given circles.
If the center of the tangent circle is connected by the segments to the centers of the two given circles,
it is immediate that the sum of the segments is the same as the difference of the radii of the two given circles.
To see this is true for sub-case 2, observe the following graph:
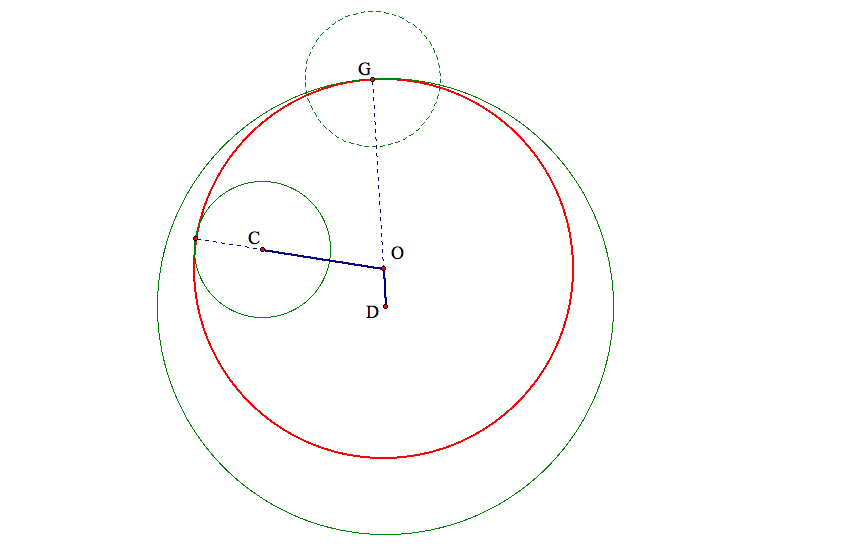
Let's call the radius of the larger given circle R, that of the smaller given circle r, and that of the tangent circle r1,
we need to show the sum of the two thick blue segments is the difference of R-r.
But |OD|=R-r1, |OC|=r1-r
Therefore, |OD|+|OC|=R-r1+r1-r=R-r.
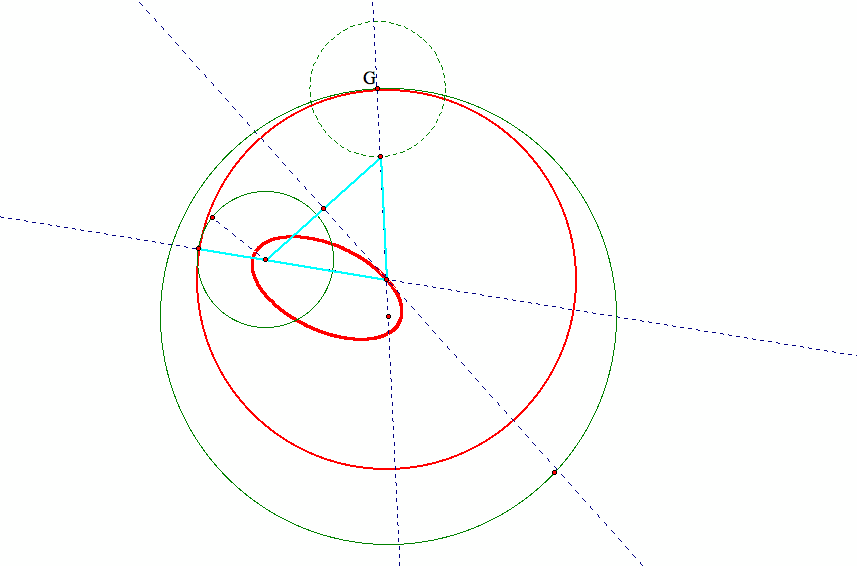
The sum of |OD| + |OC| is a constant and therefore,
we expect that the locus of the centers of the tangent circles is an ellipse with foci at the centers of the given circles.
Use the trace function of GSP, we have confirmed that the centers of the tangent circles is an ellipse for sub-case 2:
Now we want to briefly investigate two other scenarios. The first is that the two given circles intersect. The other is that the two given circles are disjoint.
Intersect Case:
If we have two given circles intersecting each other, there are two possibilities:
Possibility 1:
Starting with the above sub-case 1, we simply drag the smaller given circle until it intersects the larger given circle,
we then observe that the constructed tangent circle is inside the larger circle but outside the smaller circle.
If we trace the locus of the centers of this set of circles that are tangent to the given circles,
we find that the loci of the centers still form an ellipse, the same as in our base case:
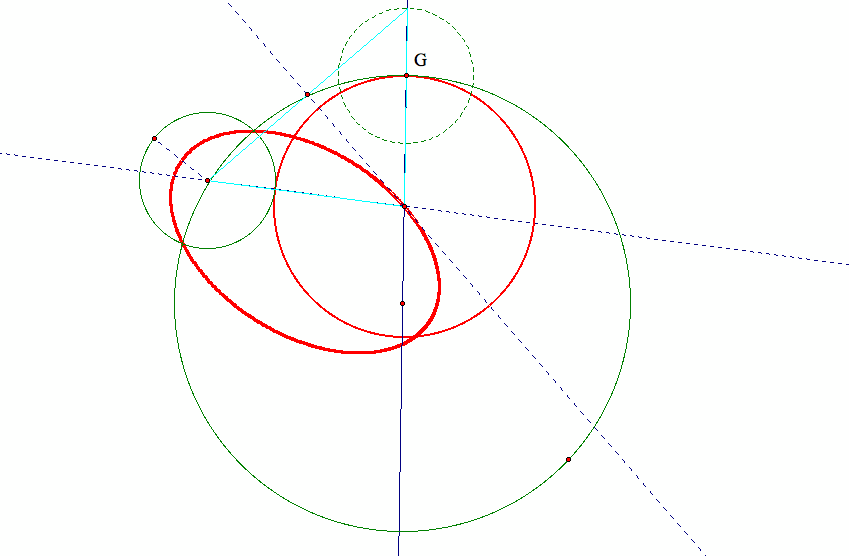
Here is why the loci of this set of circles form an ellipse as in the base cases:
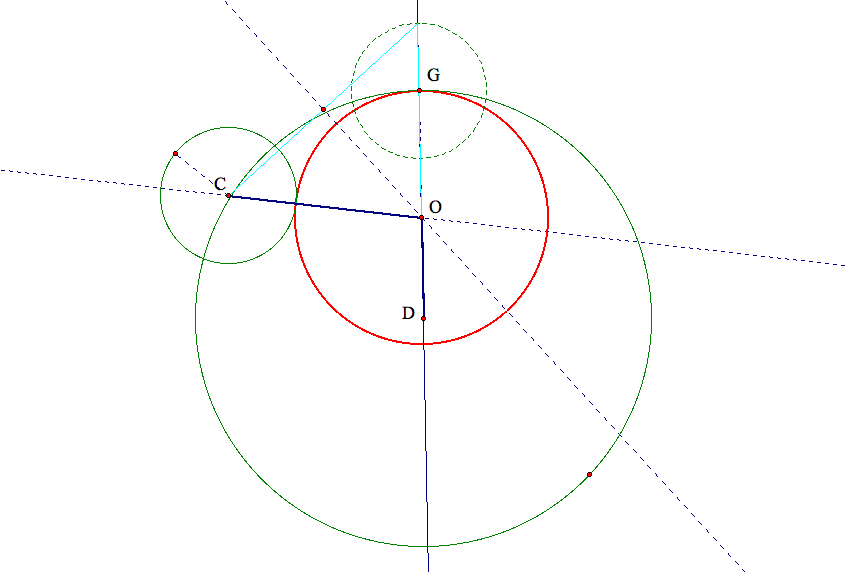
|OD|+|OC|= R-r1+r+r1=R+r,
with R is the radius of the larger given circle, r is the radius of the smaller given circle, and r1 is the radius of the constructed tangent circle.
Thus, regardless of the position of the tangent circle, the sum of the following two distances is always a constant:
(1) between the center of the tangent circle and that of the smaller given circle (i.e., the circle without the specified point of tangency in our case),
(2) between the center of the tangent circle and that of the larger given circle (i.e., the circle with the specificed point of tangency in our case)
Possibility 2:
Starting with the above sub-case 2, we simply drag the smaller given circle until it intersects the larger given circle,
we then observe that the two given circles now are both inside the constructed tangent circle.
If we trace the locus of the centers of this set of circles that are tangent to the given circles,
we find that the loci of the centers is not an ellipse anymore, but instead they form a hyperbola:
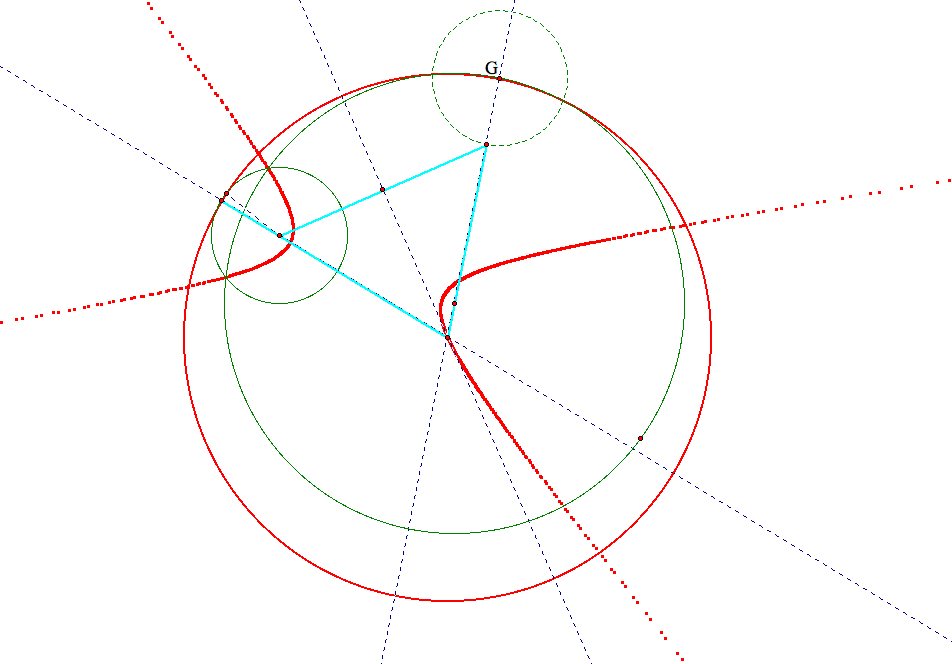
Here is why the loci of this set of circles form a hyperbola:
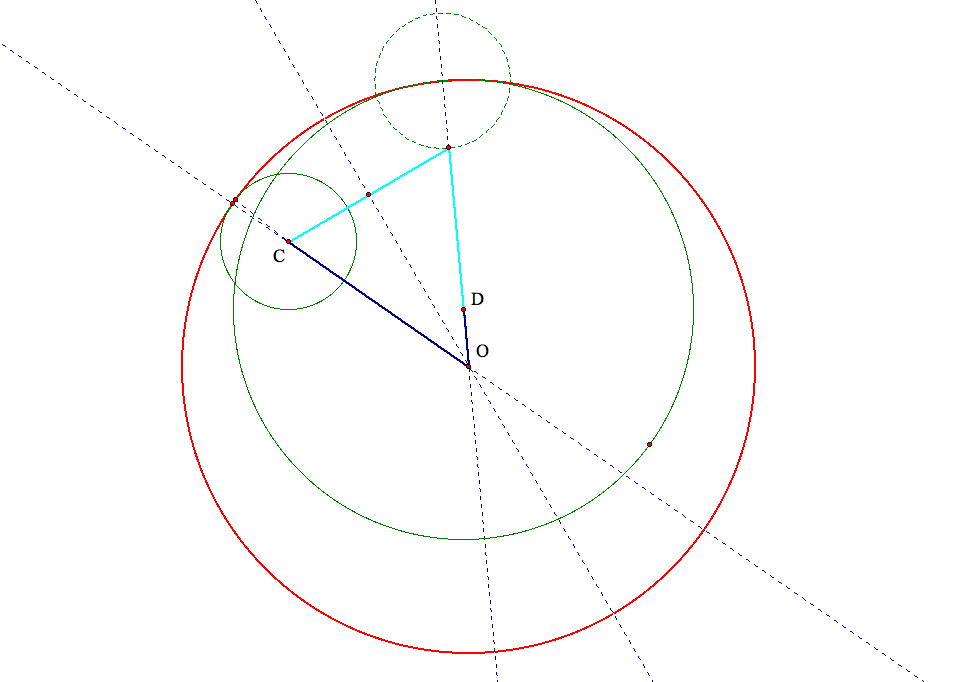
|OC|-|OD|= (r1-r)-(r1-R)=R-r,
with R is the radius of the larger given circle, r is the radius of the smaller given circle, and r1 is the radius of the constructed tangent circle.
Thus, regardless of the position of the tangent cricle,
the difference of the following two distances (marked in dark blue in the above graph) is always a constant:
(1) between the center of the tangent circle and the smaller given circle (i.e., the circle without the specified point of tangency in our case),
(2) between the center of the tangent circle and the larger given circle (i.e., the circle with the specified point of tangency in our case)
By the definition of hyperbola, we have confirmed that the loci of the centers of this set of tangent circles is indeed a hyperbola.
Disjoint Case:
If we have two given circles disjoint from each other, again there are two possibilities:
Possibility 1:
Starting with the above sub-case 1, we simply drag the smaller given circle until the two circular regions are disjoint from each other.
We then observe that the larger given circle is now inside of the constructed tangent circle, but the smaller circle is outside the constructed tangent circle.
If we trace the locus of the centers of this set of circles that are tangent to the given circles,
we find that the loci of the centers do not form an ellipse anymore, instead they form a hyperbola as in possibility 2 of the "Intersect Case".
.

Possibility 2:
Starting with the above sub-case 2, we simply drag the smaller given circle until the two circular regions are disjoint from each other.
We then observe that both given circles are outside of the constructed tangent circle.
If we trace the locus of the centers of this set of circles that are tangent to the given circles, we find that the loci of the centers do not form an ellipse anymore,
instead they form a hyperbola as in possibility 2 of the "Intersect Case".
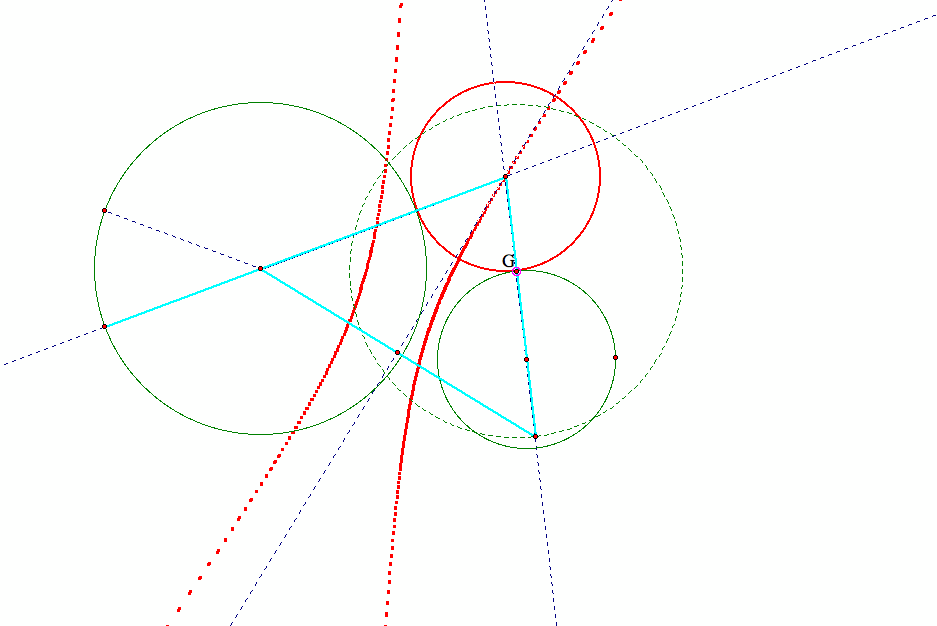
To prove that the loci of the centers of the constructed tangent circles form a hyperbola in both of the above two possibilities under "Disjoint Case",
we simply need to show that:
Regardless of the position of the tangent circle, the difference of the following two distances below is always a constant:
(1) between the center of the tangent circle and that of the smaller given circle (i.e., the circle without the specified point of tangency in our case),
(2) between the center of the tangent circle and the of the larger given circle (i.e., the circle with the specified point of tangency in our case)
The proofs are very similar to the proof we did with possibility 2 of the "Intersect Case",
I will leave these proofs for the two disjoint cases to the interested readers.
These graphs may be helpful, check them out: