Brenda King
Presenting solutions to Quadratic
equations
with a graphical structure
Introduction:
The quadratic formula,
shown below, is used to find the solution to quadratic equation in the form ax2
+ bx + c = 0.
The pattern of
roots or solutions to quadratic equations can be found by keeping two of the
parameters constant and letting the third parameter vary.
For example, if we
set a=1, c=1 and let b vary the equation becomes 1x2 + bx + 1 = y.
If we go further and let y=0, the equation can be solved depending on the assignment of parameter b.
Solving for b in the
equation 1x2 + bx + 1 = 0, we get 
.
How can this graph
be related to the quadratic formula?
Exploration:
Taking the
derivative of 1x2 + bx + 1 = 0 with
respect to x gives the line 2x + b = 0. Rewriting this becomes 
.
This line will go through the turning points of the graph as shown below and represents part of the quadratic formula.
Diagram 1
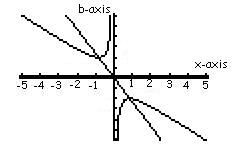
Specific Case:
If we consider a
particular value of b, say b=4, then the x-values become roots of 1x2 + 4x + 1 = 0
The graph the line on the xb plane it would look like this:
Diagram 2
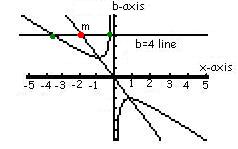
The line b=4
intersects the curve at the points 
and 
(see green dots in diagram 2).
The midpoint, m, would be located at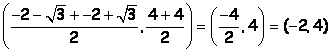 
(see red dot in diagram 2). This point also lies
on the line 2x + 4 = 0.
The distance
between the midpoint and the curve is 
.
In
General:
The point marked
in red, m, is a midpoint between the edges of the graph as shown in the
specific case when b = 4.
Solving the line
2x+b=0 for b gives a general form for the midpoint. Another way to find the midpoint would be to
work with a general point.
To find a general
point on the curve, 1x2 + bx + 1 = 0, it
is easier to use the vertex form of the equation, 
.
Derivation:
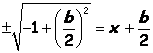
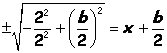
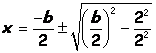
The general point
on the curve of 1x2 + bx + 1 = 0 is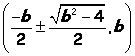 
By using this
point, the midpoint formula, 
and distance formula, 
the following results
can be found.
Midpoint 
and distance between
the midpoint and the curve = 
.
The quadratic formula, at a particular value of b, is a point on the curve 1x2 + bx + 1 = 0.
This point is the root and can be found on the line 2x+b 
distance
.
When b>2 there
would be two negative real roots.
When b=2 or b=-2,
there would be one real root.
When –2 < b
< 2, no real roots
When b < -2 . there would be two positive
real roots.