

EMAT 6680 Final Projects, Summer 2009
Bouncing Barney and Parametric Curves
by
Wenjing Li
INSTRUCTIONS:
Complete each of the following parts. Part One is merely finishing off the write-ups for the semester. Part Two should be new web page items. Part Three is the course evaluation.
Part One
Review your Write-ups 1 to 12. Revise as you wish to reach the point where you feel that, collectively, the 12 write-ups represent your best work for the course. They are an elctronic portofolio of your work.
Part Two
Complete a Write-up on your Web Page for each of A and B below. This should be individual work.
A. Bouncing Barney. We discussed this investigation in class. Your challenge now is to prepare a write-up on it, exploring the underlying mathematics ideas and conjectures.
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.
I assume some GSP sketches and explorations will be useful as well as proofs of the conjectures. A highly regarded write-up will examine the extensions and interpretations of this exploration. For example, as we discussed in class --
Will Barney always return to his starting point? If so, will Barney always travel the same distance? Does the path create a pattern of similar triangles? Where might his starting point be so that the path would create congruent triangles? What if Barney started at a point inside the triangle? Anything special about the path if he starts at the centroid? the othocenter?
Extend the sides of the triangle and let Barney begin his journey from a point outside the triangle. His path is slightly redefined -- rather than "bouncing" when he comes to a wall, he crosses the wall to change direction and continues to travel a path parallel to a side of the triangle. Construct a GSP image and explore.
The problem is rather open-ended. Don't give up on it too early.
Let us first explore the path that Barney's walk in the trangular room ABC.
Case A. the starting point D is on the segment BC
A1. the starting point D is an arbitrary point on one of the segment BC
Barney walks from a point D on BC parallel to AC.
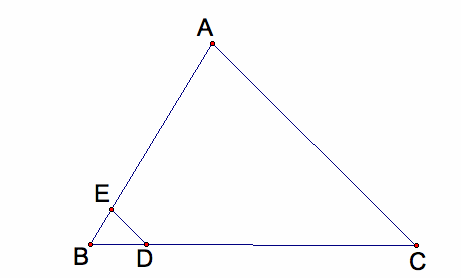
When Barney reaches a point E on AB, he turns and walks parallel to BC.
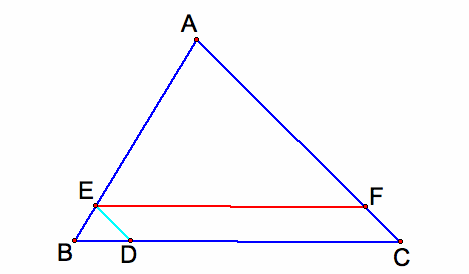
When Barney reaches the point F on the side AC, he turns and walks parallel to AB.
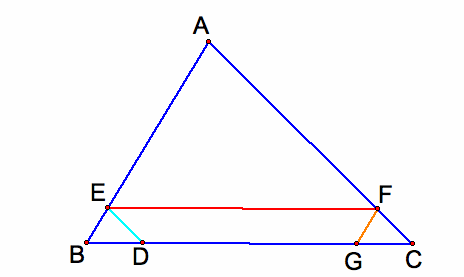
Similarly when Barney reaches the point G on the side BC, he turns and walks parallel to AC.
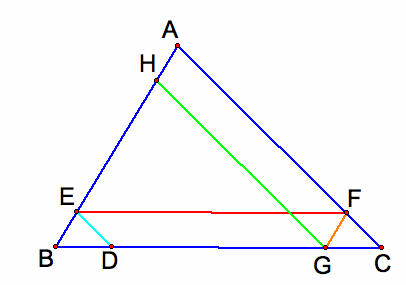
When Barney reaches the point H on the side AB, he turns and walks parallel to BC.
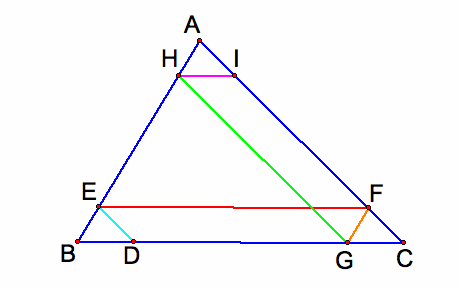
When Barney reaches the point I on the side AC, he turns and walks parallel to AB and finally he return back to the starting point D.
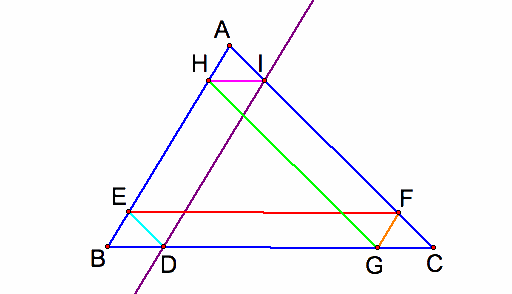
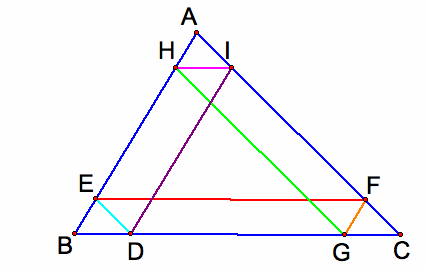
Claim 1: Barney will eventually return to his starting point D on the segment BC.
Proof: Since EF is parallel to BCand DE is parallel to CF
Thus EFCD is a parallelogram and DE=CF
Since EB is parallel to FG, DE is parallel to CF and DE=CF,
Hence the triangle EBD and the triangle FGC are congruent to each other.
Similarly, HGCI is a parallelogram implies that
HI=GC
The triangle EBD and the triangle FGC are congruent to each other implies that
BD=GC
Hence HI=BD
Let J be the point that Barney will eventually return to on the segment BC.
Then HBJI is a parallelogram impies that
HI=BJ
Since HI=BD
Thus BJ=BD
Hence J=D and Barney will eventually return to the starting point D on the segment BC.
Claim 2: The distance that Barney travels is equal to the parameter of the triangle ABC.
Proof: Let d be the distance Barney will travel. Then we have
Total distance d
=DE+EF+FG+GH+HI+ID
=FC+DC+BE+AF+BD+AE
=(AE+EB)+(BD+DC)+(AF+FC)
=AB+BC+AC
=the parameter of the triangle ABC
There will be five times Barney reach a wall before returning to his starting point. The total distance of the walk is the same as the parameter of the triangle ABC.
A2. the starting point D is the midpoint of the segment BC
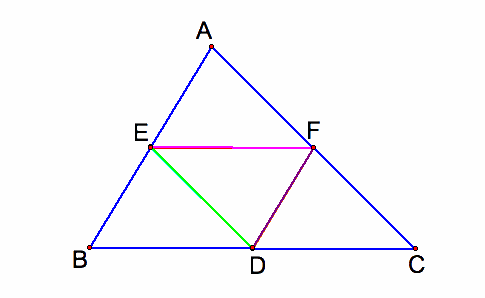
If the starting point is the midpoint of the segment BC, then Barney will reach a wall two times before returning to his starting point.
Claim: The distance Barney that travels is equal to half of the parameter of the triangle ABC.
Proof: Since D is the midpoint of BC and DF is parallel to AB
thus DF has length half of the the length AB
Simmilarly, since E is the midpoint of AB and DE is parallel to AC
thus DE has length half of the the length AC
Since F is the midpoint of AC and EF is parallel to BC
thus EF has length half of the the length AB
Hence the total distance d
=DE+EF+FD
=(1/2)AC+(1/2)BC+(1/2)AB
=(1/2)(AB+BC+AC)
(1/2)(parameter of the triangle ABC)
Therefore the distance Barney travels is equal to half of the parameter of the triangle ABC.
Barney will always return to his starting point. The distance Barney travels is equal to half of the parameter of the triangle ABC. The path creates a pattern of similar triangles. If his starting point is the midpoint of one side of the triangle, then the path would create congruent triangles. The triangle AEF is congruent to the triangle EBD. The triangle AEF is congruent to the triangle FDC. The triangle AEF is congruent to the triangle DEF. Hence the four triangles AEF, EBD, FDC, DEF are congruent.
A3. the starting point D is one of the two points of the trisection that divide the segment BC into three equal length segments
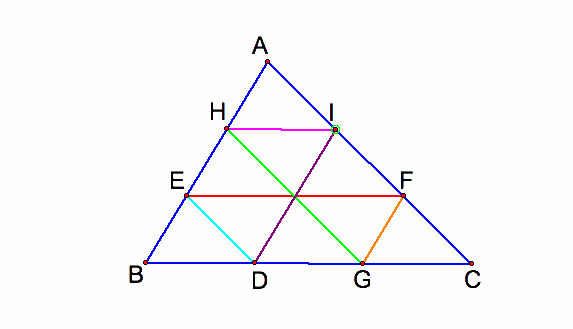
Barney will always return to his starting point. Similarly to the case A1, Barney will travel the distance which is the same as the parameter of the triangle ABC. The path create a pattern of similar triangles. If his starting point is the starting point D is one of the two points of the trisection that divide the segment BC into three equal length segments, then the path would create congruent triangle AHI, triangle HEJ, triangle EBD, triangle JDG, triangle FGC, triangle IJF, triangle JIH, triangle DGE, and triangle DFG.
A4. the starting point D is one of the vertex B
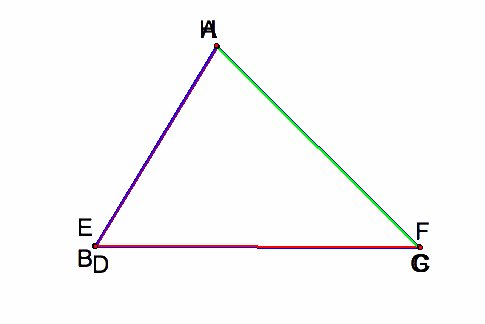
Barney will return to his starting point? Barney will travel the distance which is the same as the parameter of the triangle ABC and the path is along the triangle ABC.
Case B. the starting point D is inside the triangle ABC
B1. the starting point D is an arbitrary point inside the triangle ABC
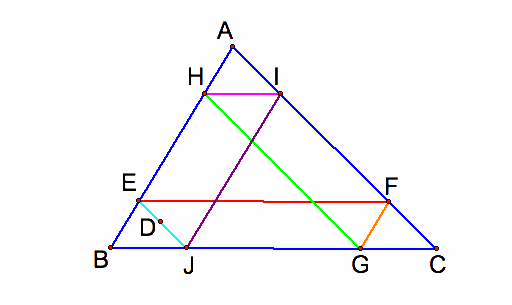
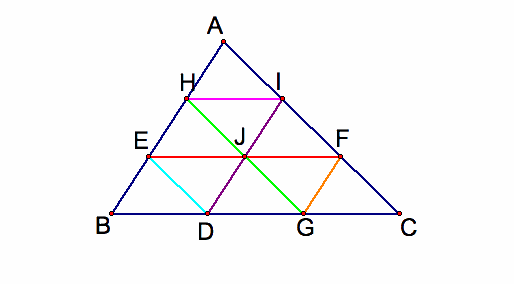
Barney will always return to his starting point D? Similarly to case A1, there will be five times Barney reach a wall before returning to his starting point. The total distance of the walk is the same as the parameter of the triangle ABC. The path create a pattern of similar triangles. The triangle AHI is congruent to the triangle EBJ. The triangle AHI is congruent to the triangle FGC.
B2. the starting point D is the centroid of the triangle ABC
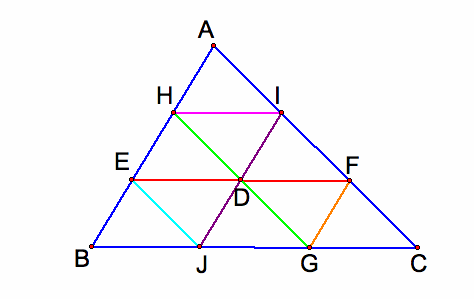
There will be five times Barney reach a wall before returning to his starting point. If the starting point D is the centroid of the triangle ABC, then Barney will always return to his starting point. Similarly to the case A3, Barney will travel the distance which is the same as the parameter of the triangle ABC. The path create a pattern of similar triangles. If his starting point is the starting point D is the centroid of the triangle ABC, then the path would create congruent triangles. The triangle AHI, triangle HEJ, triangle EBD, triangle JDG, triangle FGC, triangle IJF, triangle JIH, triangle DGE, and triangle DFG are all congruent to each other. The path will pass through the centroid D.
B3. the starting point D is the othocenter of the triangle ABC
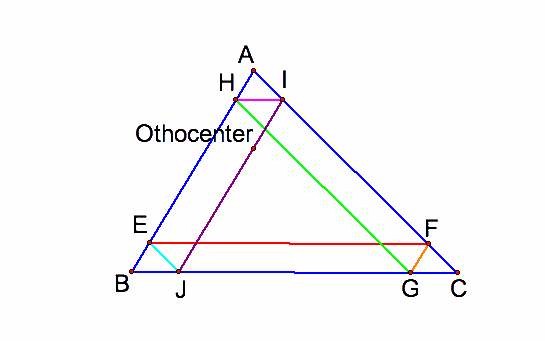
There will be five times Barney reach a wall before returning to his starting point. If the starting point D is the othocenter of the triangle ABC, then Barney will always return to his starting point. Barney will travel the distance which is the same as the parameter of the triangle ABC. The path create a pattern of similar triangles. If his starting point is the starting point D is the othocenter of the triangle ABC, then the path would create congruent triangles. The triangle AHI, triangle EBJ, triangle FGC are congruent to each other. Compare to the case B2 of centroid, the difference is that if the starting point D is the centroid of the triangle ABC then the path will pass through the centroid. But if the starting point D is the othocenter of the triangle ABC, then the path will not pass through the othocenter.
Case C. the starting point D is outside the triangle ABC
C1. the starting point D is on the line BCwhich is outside the triangle ABC
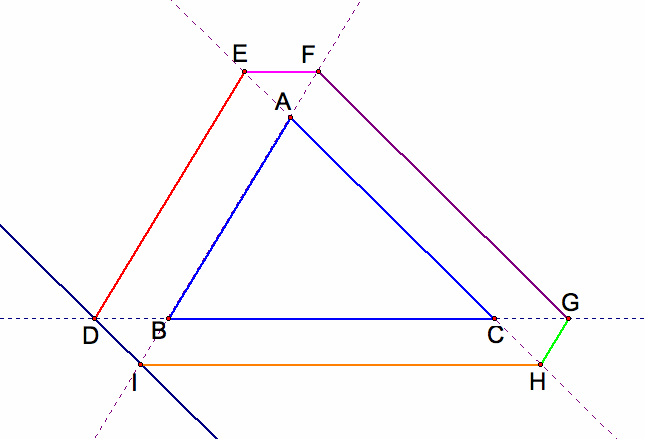
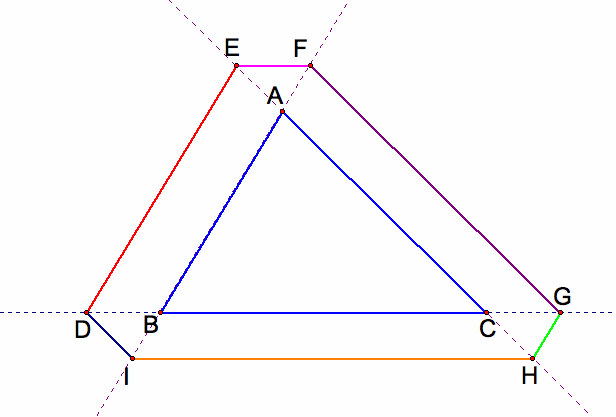
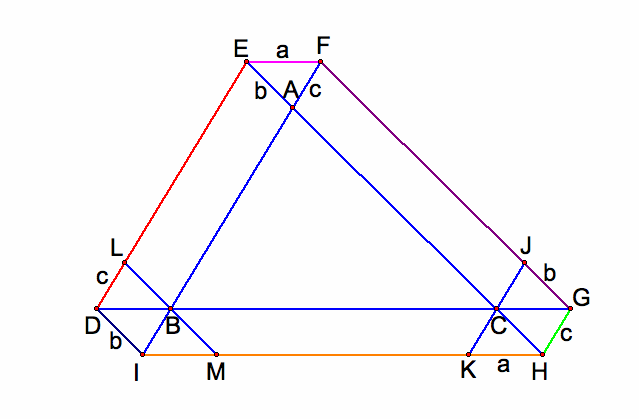
We now extend the sides of the triangle ABC and let Barney begin his journey from a point outside the triangle. If the starting point D is on the line BC but outside the segment BC, the path is slightly redefined, rather than "bouncing" when he comes to a wall, he crosses the wall to change direction and continues to travel a path parallel to a side of the triangle. There will be six times Barney reach the extended side of a wall before returning to his starting point. Barney will return to the starting point D. The path create a pattern of similar triangles and also congruent triangles, triangle AEF, triangle IBD, triangle HGC. The distance that Barney travels is greater than the parameter of the triangle ABC.
Claim: The distance that Barney travels is equal to the sum of the parameter of the triangle ABC and twice the sume of a, b,c, where a is the length of segment EF, b is the length of segment AE, c is the length of segment AF.
Proof: Since EL is parallel to AB and AE is parallel to BL
Thus ABLE is a parallelogram and AB=EL.
Similarly, BCKI is a parallelogram implies that
BC=KI
ACJF is a parallelogram implies that
AC=FG
Since DL is parallel to AF, AE is parallel to BL and EF=BD,
Hence the triangle AEF and the triangle LBD are congruent to each other.
Thus DL=AF=c
Similarly, JG=AE=b, GH=AF=c, KH=FE=C, DI=EA=b.
HI=GC
Hence the total distance d
=DE+EF+FG+GH+HI+ID
=DL+LE+EF+FJ+JG+GH+HK+KI
=c+AB+a+AC+b+c+a+BC+B
=(AB+BC+AC)+2(a+b+c)
=(parameter of the triangle ABC)+2(a+b+c)
C2. the starting point D is an arbitrary point outside the triangle ABC
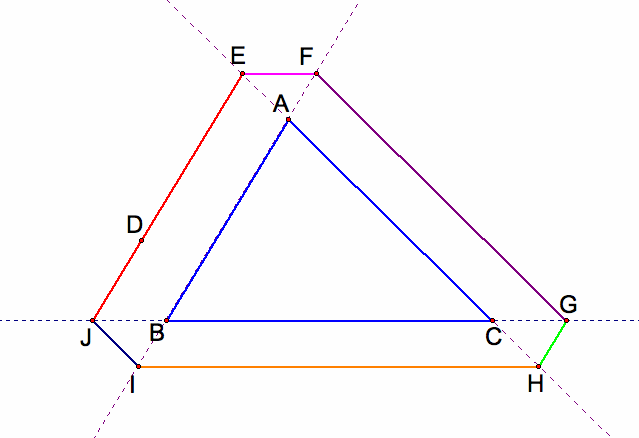
If the starting point D is an arbitrary point outside the triangle ABC, then there will be six times Barney reach the extended side of a wall before returning to his starting point D. Barney will return to the starting point D. The path create a pattern of similar triangles and also congruent triangles, triangle AEF, triangle IBJ, triangle HGC are congruent to each other. The distance that Barney travels is greater than the parameter of the triangle ABC. The distance that Barney travels is equal to the sum of the parameter of the triangle ABC and twice the sume of the length of segment EF and the length of segment AE and the length of segment AF.
To summarize, Barney will always return to his starting point. The path creates a pattern of similar triangles and congruent triangles. The distance Barney travels is not always the same and it depends on the starting point. If the starting point is the midpoint of one side of the triangle or the centroid of the triangle, then the distance Barney travels is equal to half of the parameter of the triangle ABC. If the starting point is outside the triangle ABC, then the distance that Barney travels is equal to the sum of the parameter of the triangle ABC and twice the sume of the length of segment EF and the length of segment AE and the length of segment AF. For other cases, the distance that Barney travels is equal to the sum of the parameter of the triangle ABC.
B.
Complete a Write-up on your Web Page for one additional investigation, chosen from Assignment 0 through Assignment 12. Clearly it should be an investigation other than one you have written up before. This should be individual work.
We choose to do the assignment 10 parametric curves problem 11
EMAT 6680 Assignment 10:
Parametric Curves
11. Investigation. Consider the parametric equations
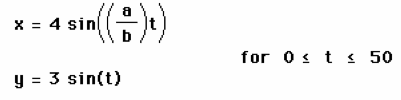
Graph these for
![]()
Describe fully. You may have to increase the range of t for the larger fractions. This class of parametric curves are called the Lissajous curves. Compare with
x = sin((a)t)
y = sin((b)t)
We graph the parametric equations
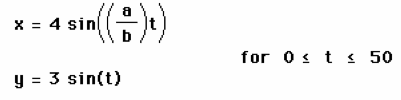
1.For a/b=1, we get a line segment with x-coordinate between -4 to 4 and y-coordinate between -3 to 3.
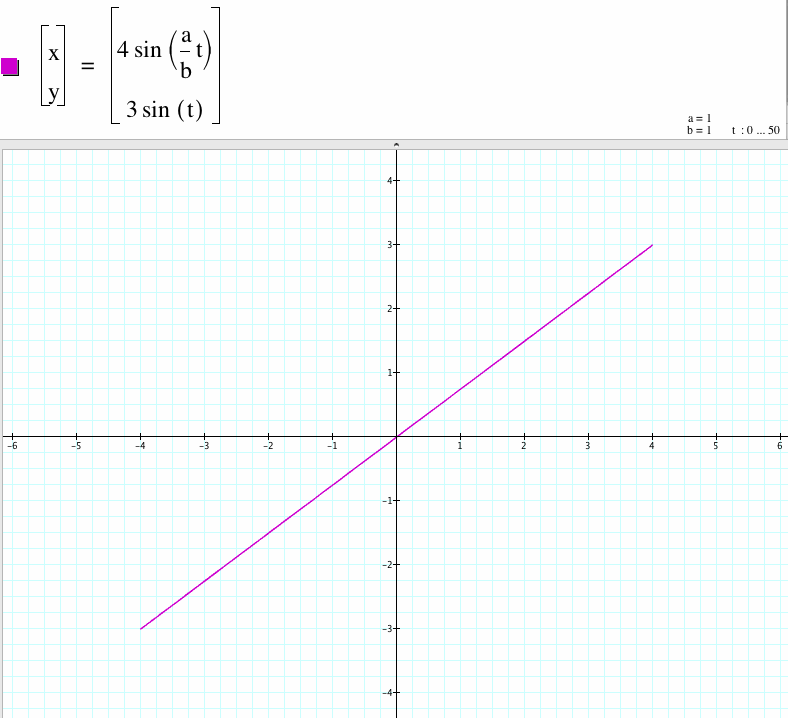
2. For a/b=2, we have a curve with two cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
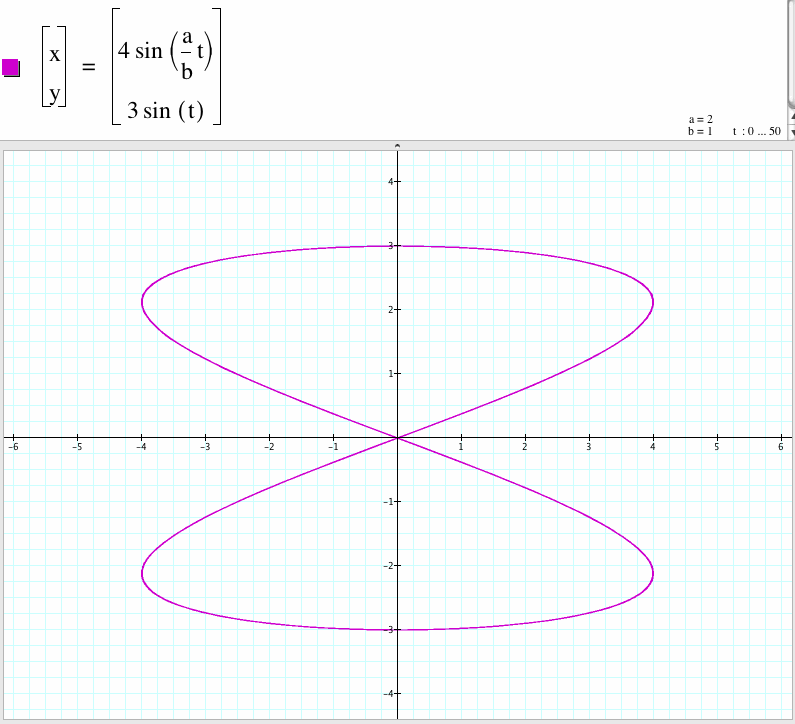
3. For a/b=4, we get a curve with four cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
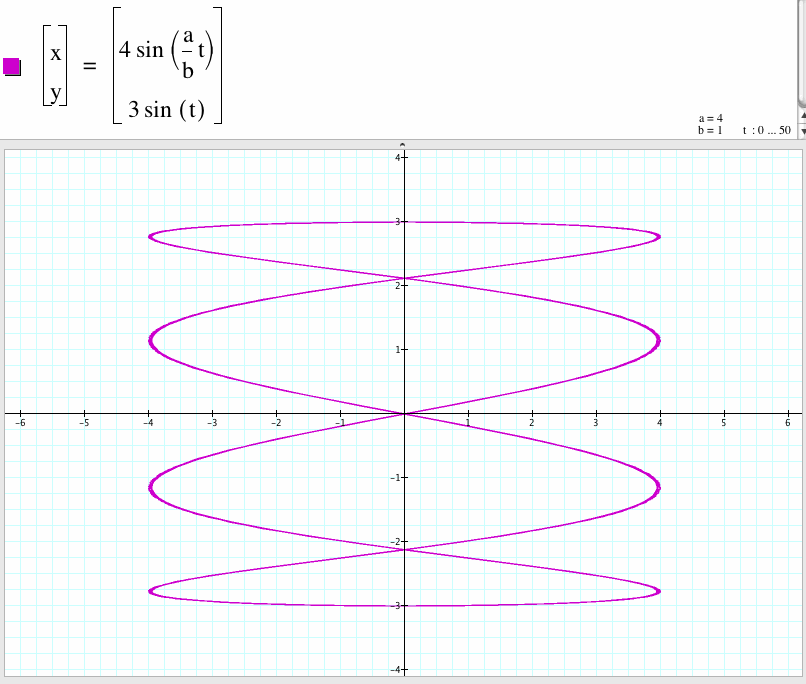
4. For a/b=6, we get a curve with six cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
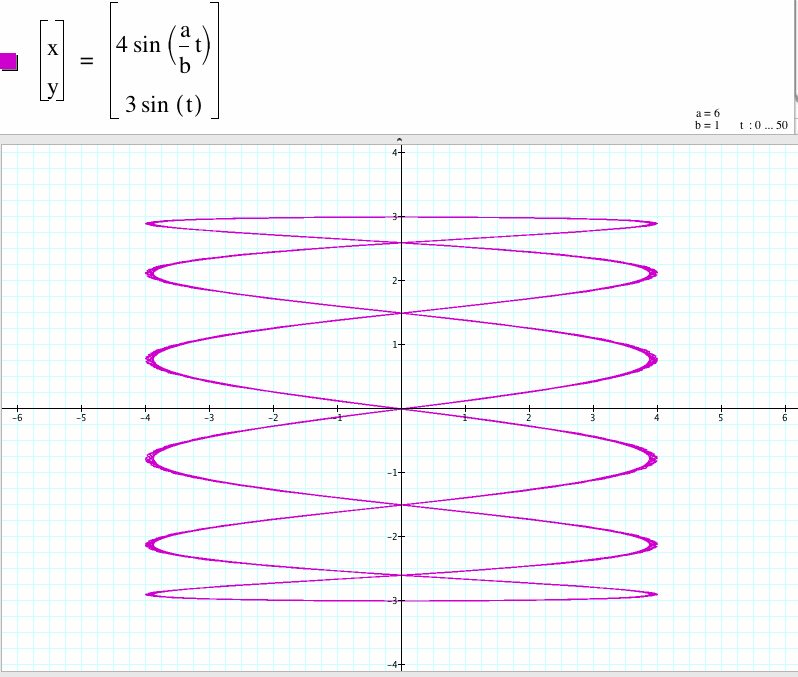
In general, if a/b is an even integer n, then the graph of this parametric equations are curves with n cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
5. For a/b=3, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3.
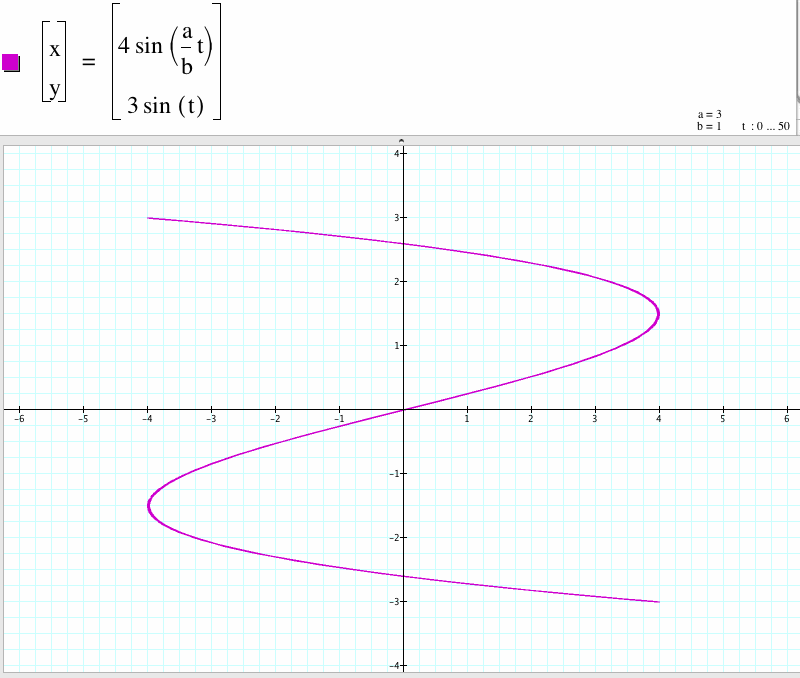
6. For a/b=5, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3.
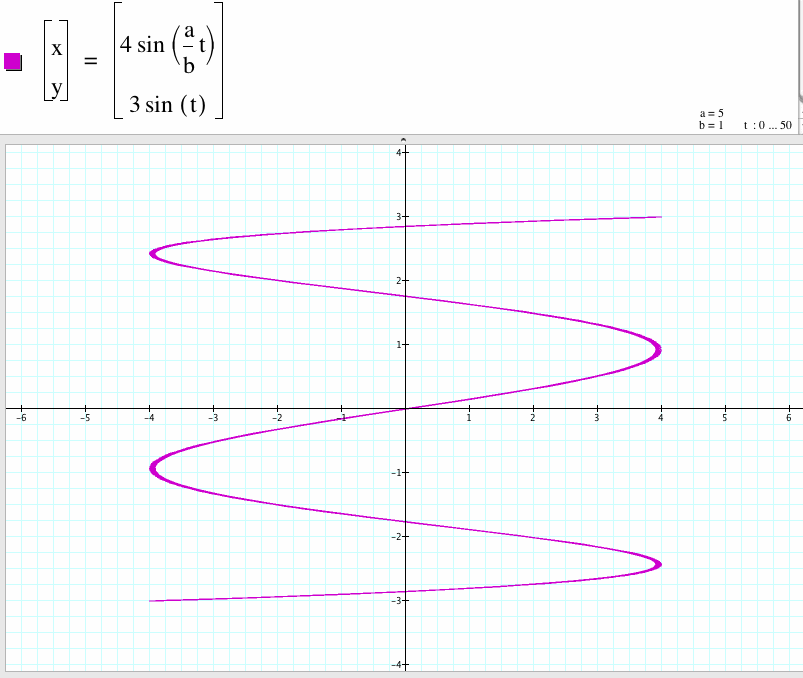
7. For a/b=7, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3.
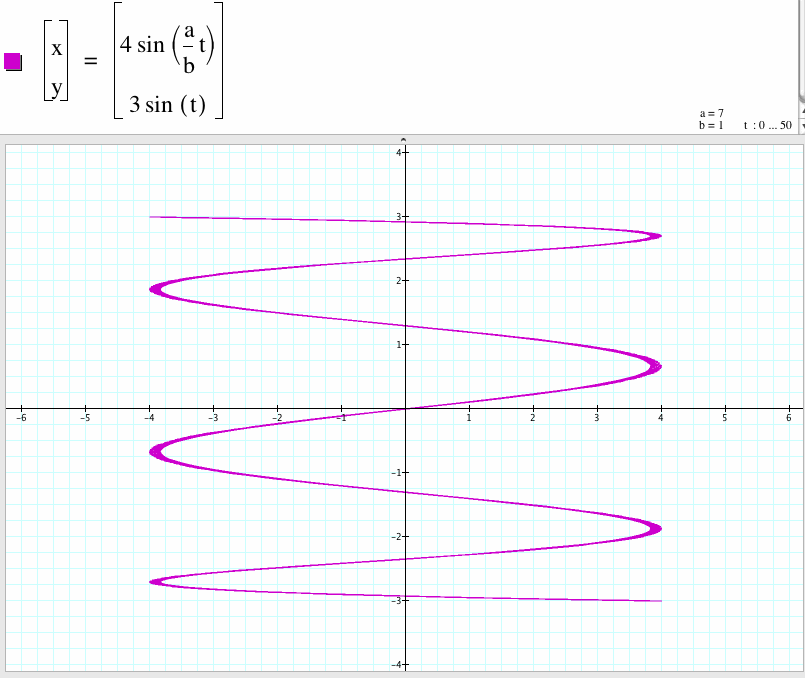
In general, if a/b is an odd integer, then the graph of this parametric equations are curves which are open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3.
Now let us investigate what the graph will look like if a/b is not integers.
We let a/b to be one divided by an even integer.
8. For a/b=1/2, we have a curve with two cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3. Compare to the case a/b=2, the shape of this graph rotates 90 degree.
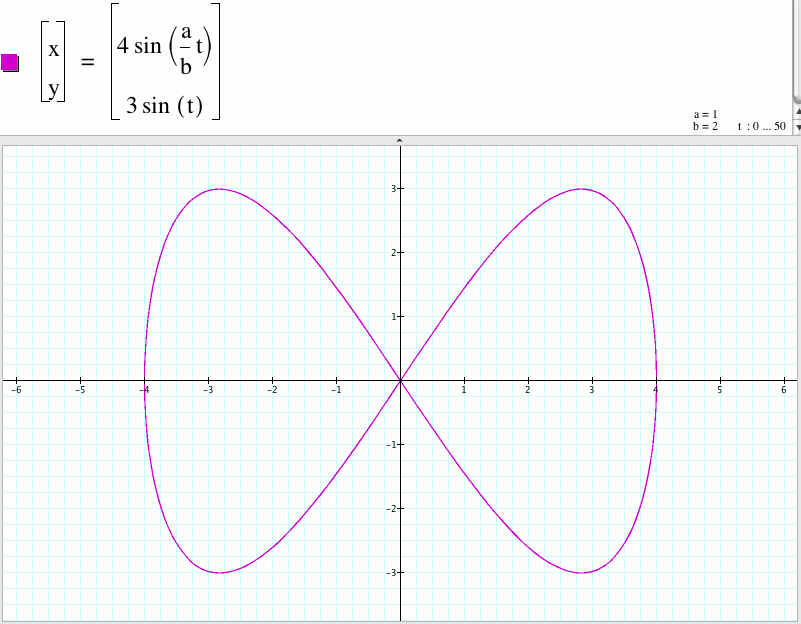
9. For a/b=1/4, we have a curve with four cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3. Compare to the case a/b=4, the shape of this graph rotates 90 degree.
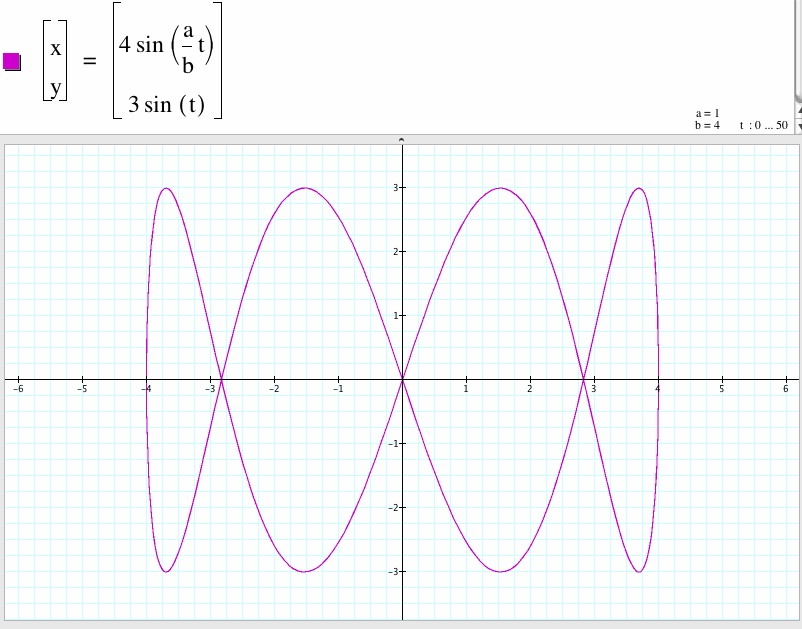
10. For a/b=1/6, we have a curve with six cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3. Compare to the case a/b=6, the shape of this graph rotates 90 degree.
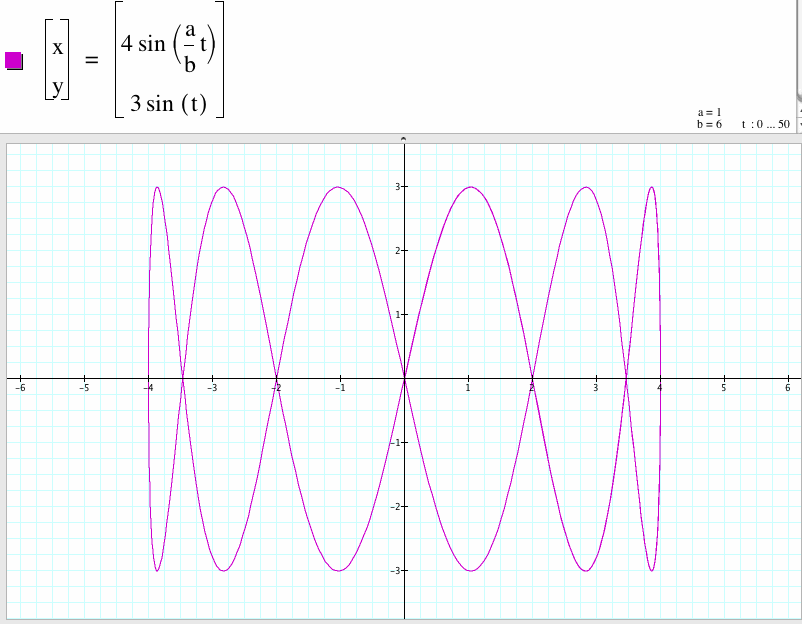
In general, if a/b is one divides an even integer n, then the graph of this parametric equations are curves with n cycles which x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3. If we compare the graph with the integer cases respectively, we found that the corresponding graph rotates 90 degree.
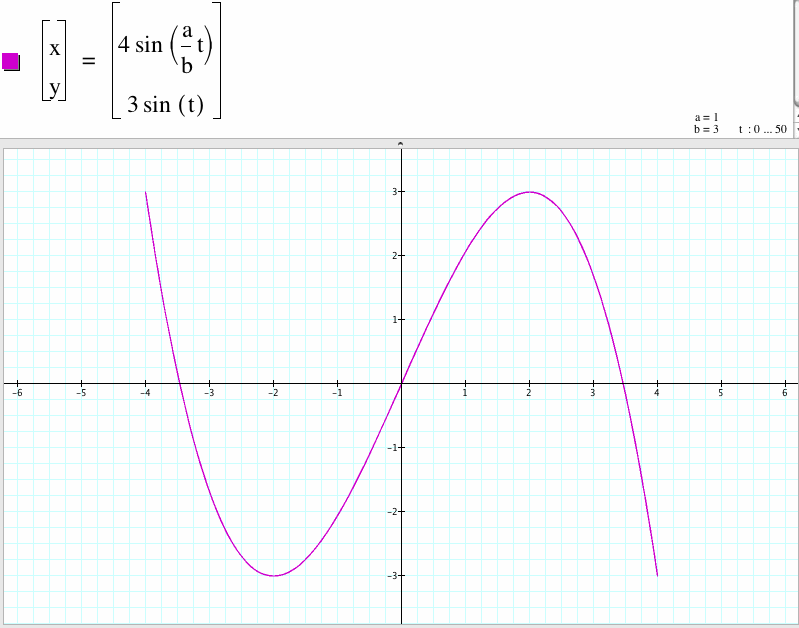
11. For a/b=1/3, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3. Compare to the case a/b=3, the shape of this graph rotates 90 degree.
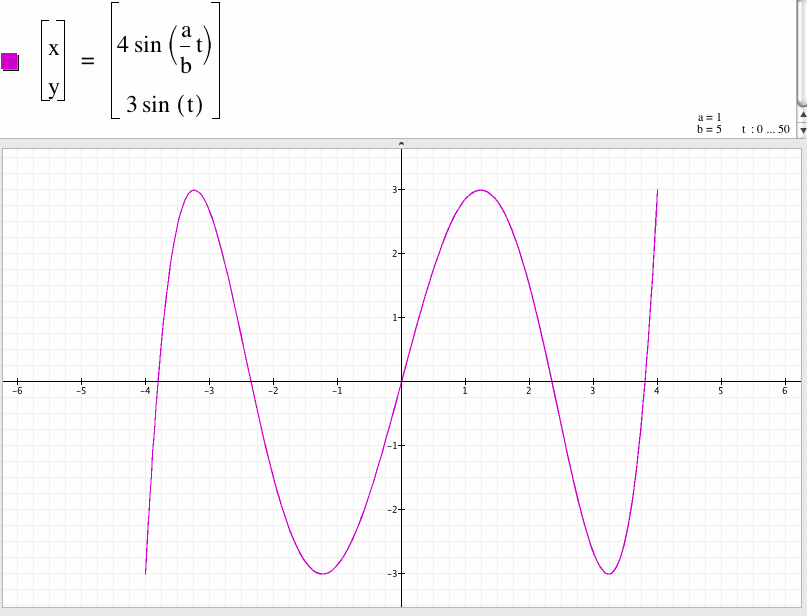
12. For a/b=1/5, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3. Compare to the case a/b=5, the shape of this graph rotates 90 degree.
13. For a/b=1/7, we get a curve which is open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3. Compare to the case a/b=7, the shape of this graph rotates 90 degree.
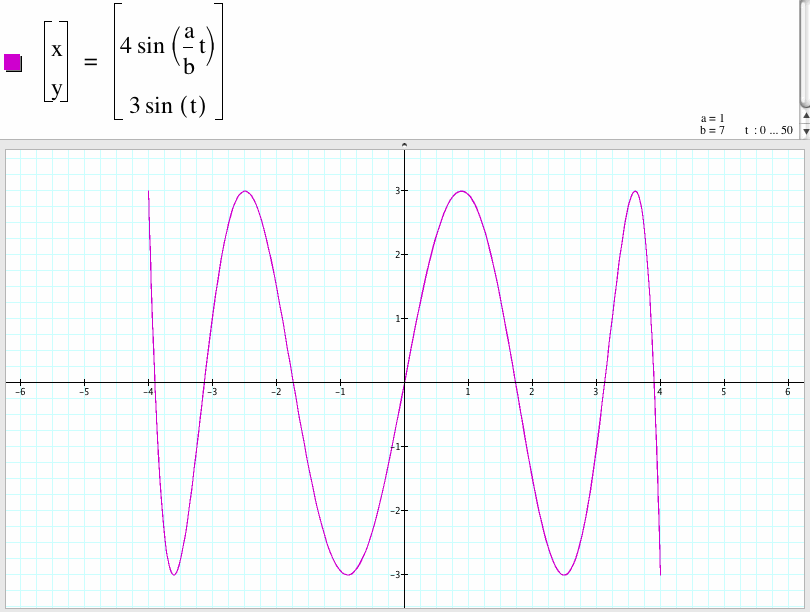
To summarize, if a/b is one divides an odd integer n, then the graph of this parametric equations are curves which are open and x-coordinate between -4 to 4 and y-coordinate between -3 to 3. If we compare the graph with the integer cases respectively, we found that the shape of the corresponding graph rotates 90 degree.
14. For a/b=2/3
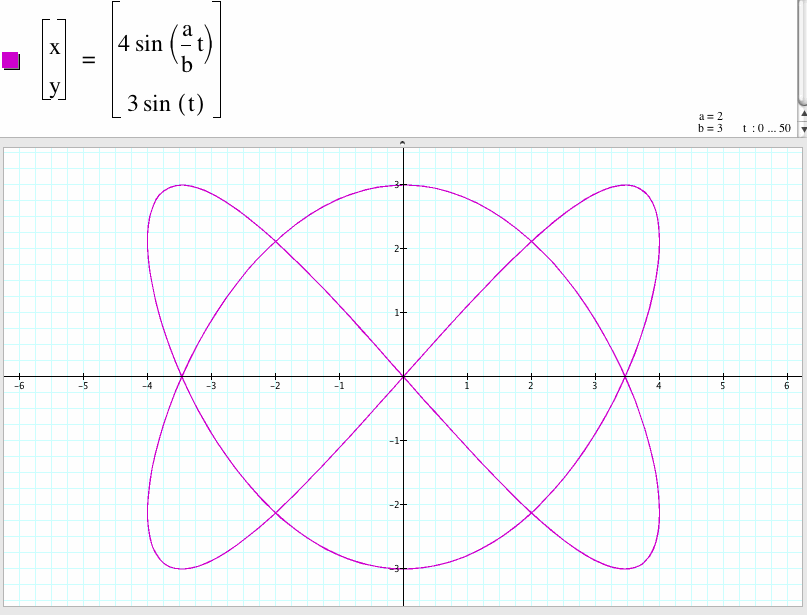
15. For a/b=3/2
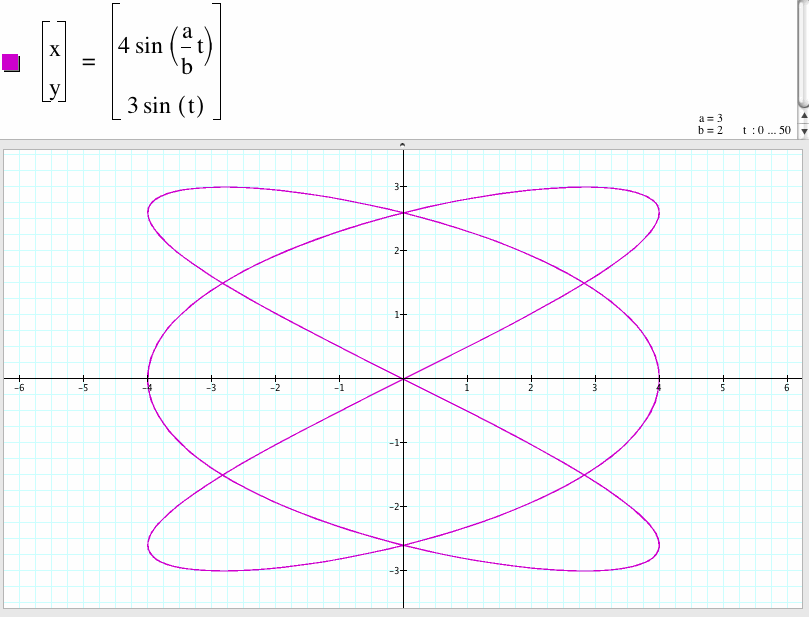
We compare the graph of the case a/b=2/3 and the case a/b=3/2 and found that the shape of the graph of the case a/b=3/2 is the shape of the graph of the case a/b=2/3 rotates 90 degree.
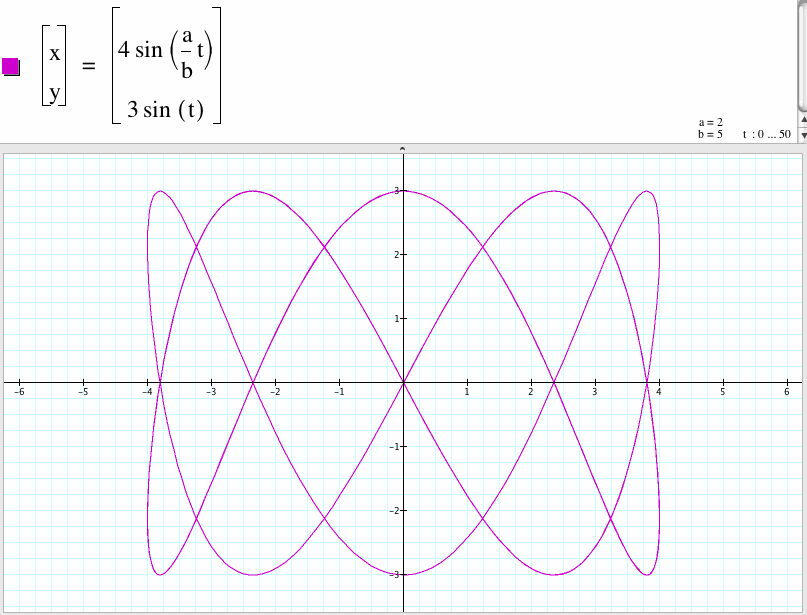
16. For a/b=2/5
17. For a/b=5/2
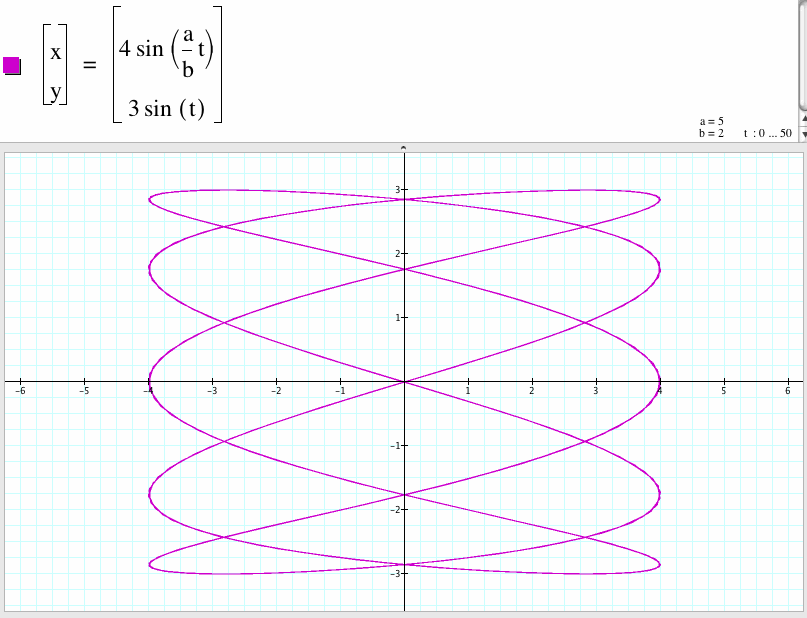
We compare the graph of the case a/b=2/5 and the case a/b=5/2 and found that the shape of the graph of the case a/b=5/2 is the shape of the graph of the case a/b=2/5 rotates 90 degree.
18. For a/b=3/5
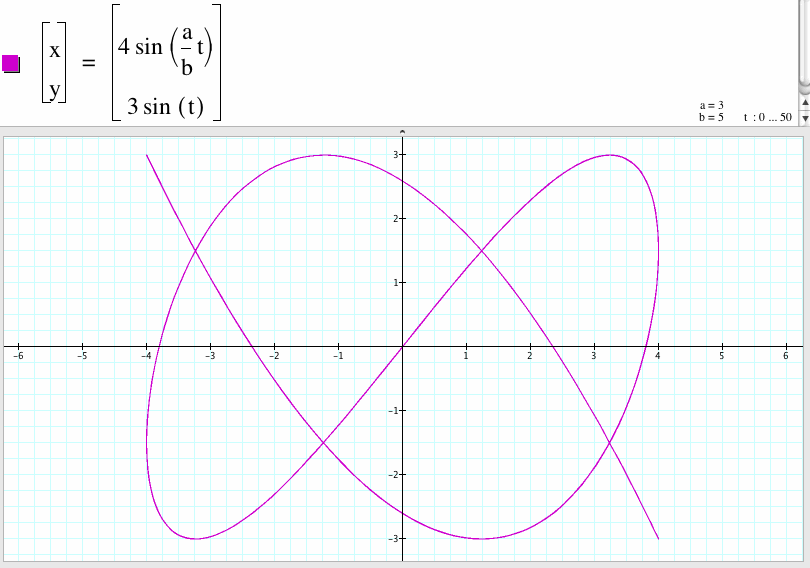
19. For a/b=5/3
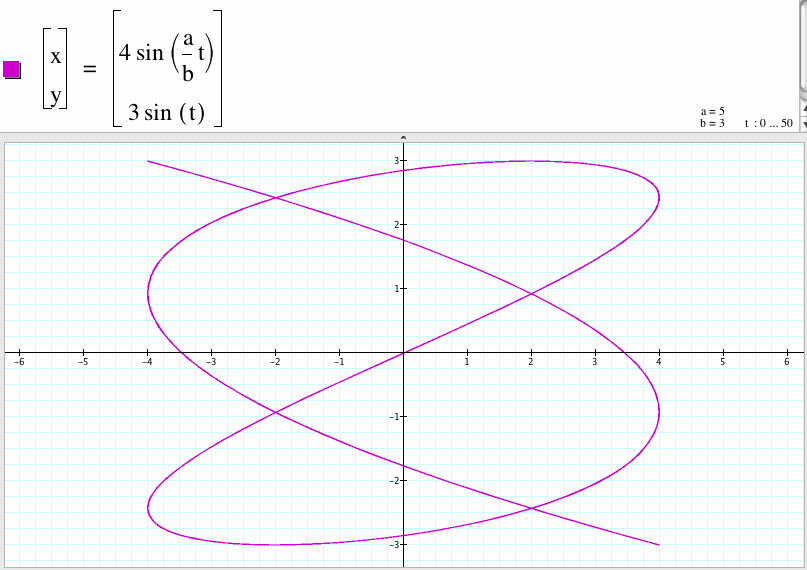
We compare the graph of the case a/b=5/3 and the case a/b=3/5 and found that the shape of the graph of the case a/b=3/5 is the shape of the graph of the case a/b=5/3 rotates 90 degree.
20. For a/b=12/13
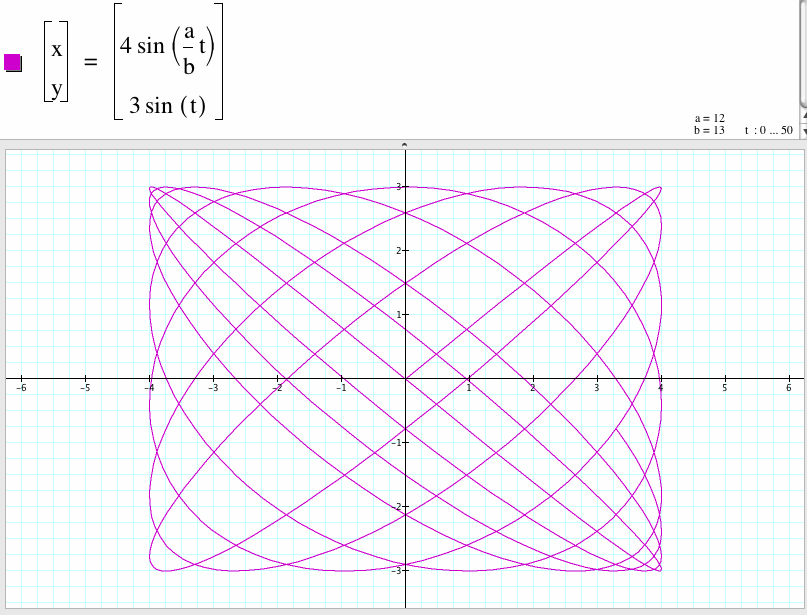
21. For a/b=13/12
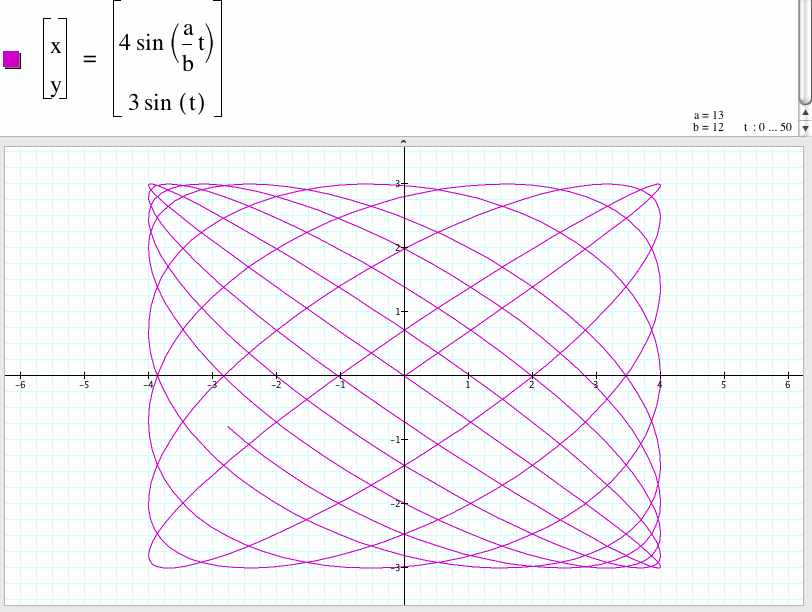
We compare the graph of the case a/b=12/13 and the case a/b=13/12 and found that the shape of the graph of the case a/b=13/12 is the shape of the graph of the case a/b=12/13 rotates 90 degree.
In general, for the two cases of a/b are reciprocal to each other, then the shape of the graph of one case is the shape of the graph of the other case rotates 90 degree.
We now compare the graph of parametric equations
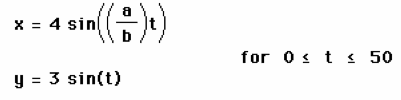
with the graph of parametric equations
x = sin((a)t)
y = sin((b)t)
1. For a/b=2, the graph of the two parametric equations have the same shape with different ranges of x and y . The two curves are both have two cycles. The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
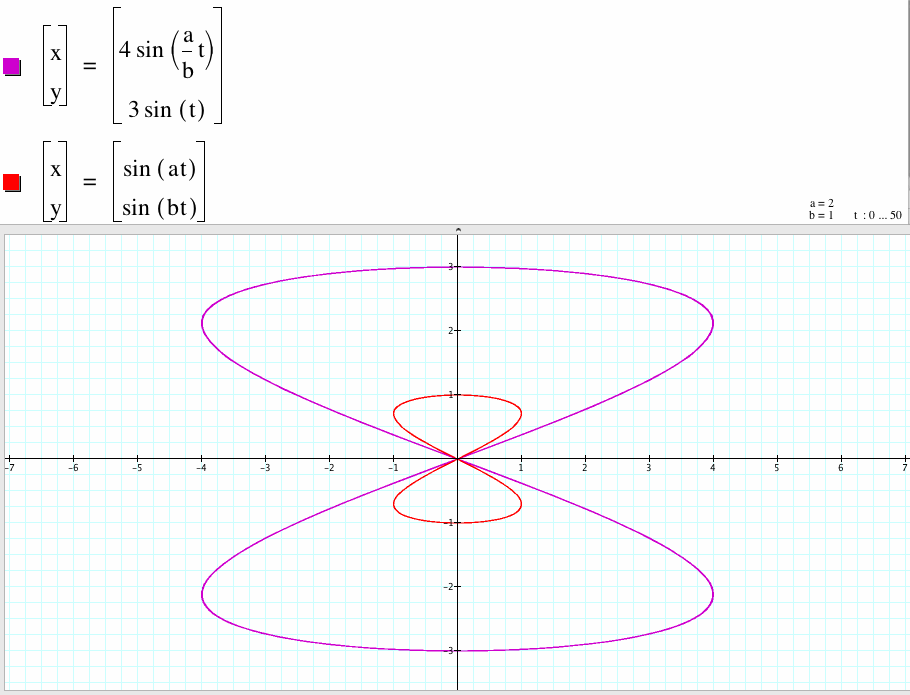
2. For a/b=1/2, the graph of the two parametric equations have the same shape with different ranges of x and y . The two curves are both have two cycles. The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
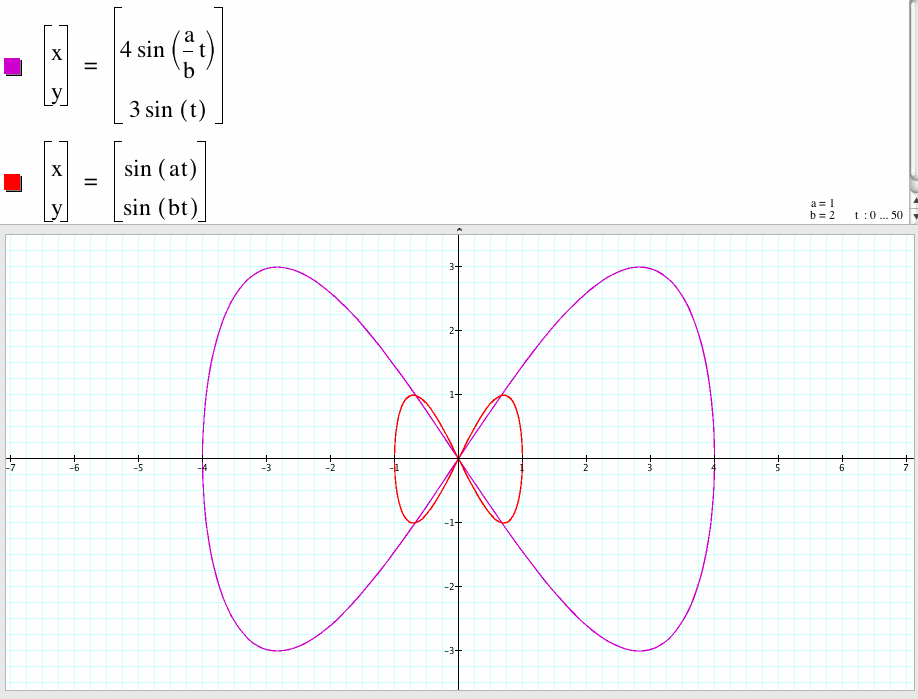
3. For a/b=3, the graph of the two parametric equations have the same shape with different ranges of x and y . The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
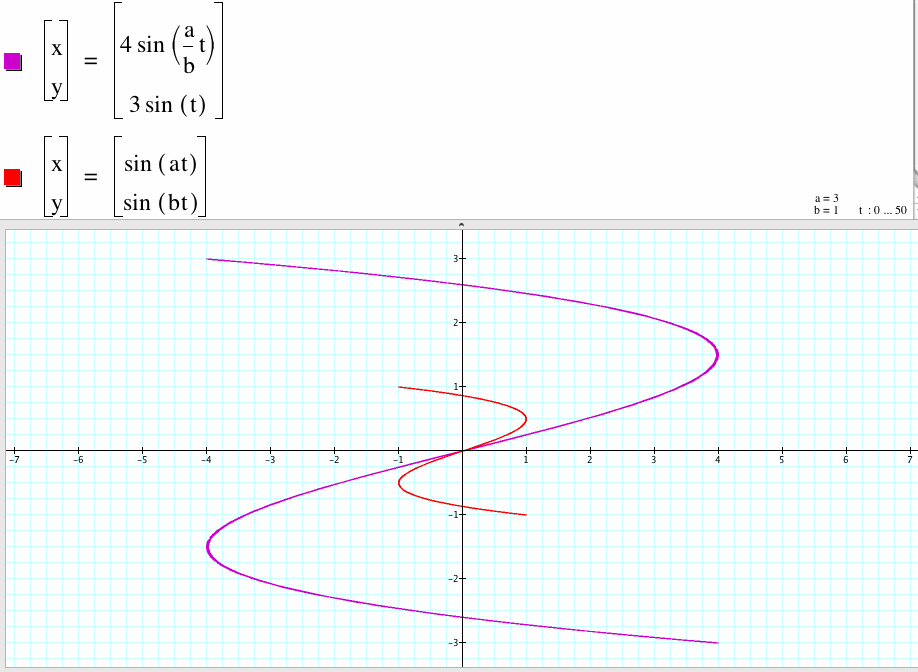
4. For a/b=1/3, the graph of the two parametric equations have the same shape with different ranges of x and y . The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
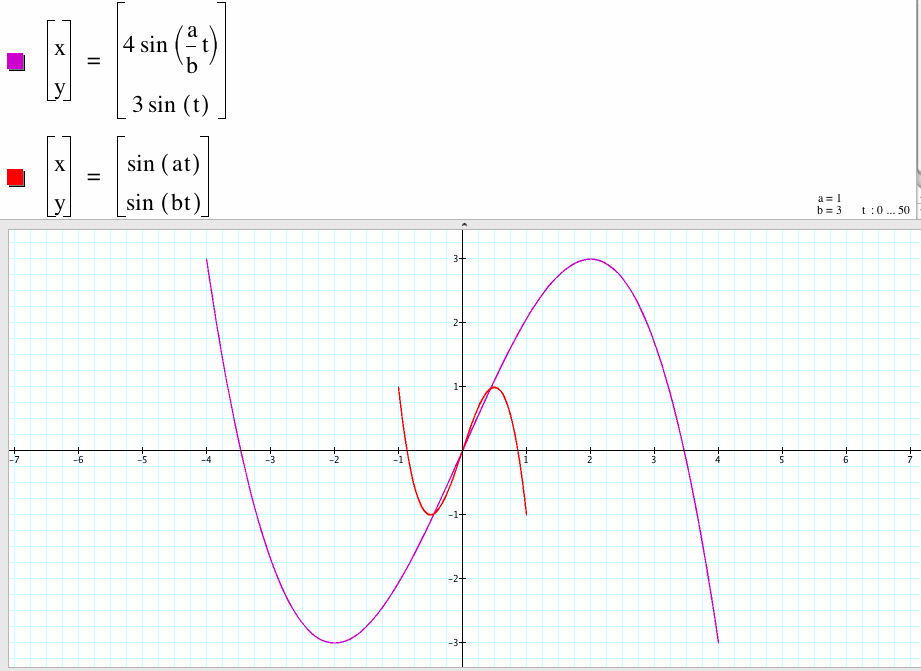
5. For a/b=2/3, the graph of the two parametric equations have the same shape with different ranges of x and y . The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
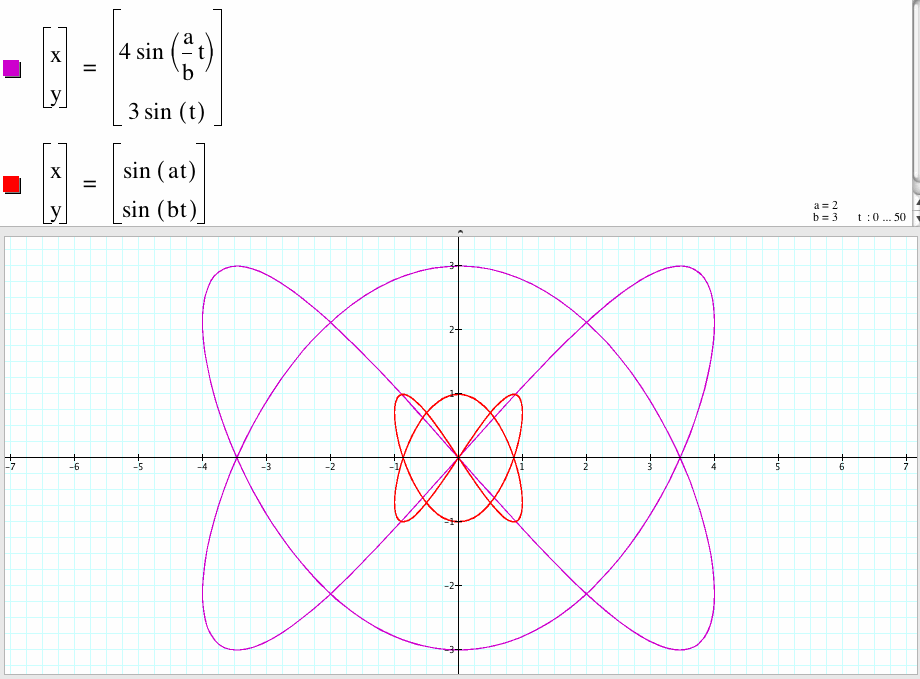
6. For a/b=3/2, the graph of the two parametric equations have the same shape with different ranges of x and y . The bigger curve x-coordinate is between -4 to 4 and y-coordinate is between -3 to 3.
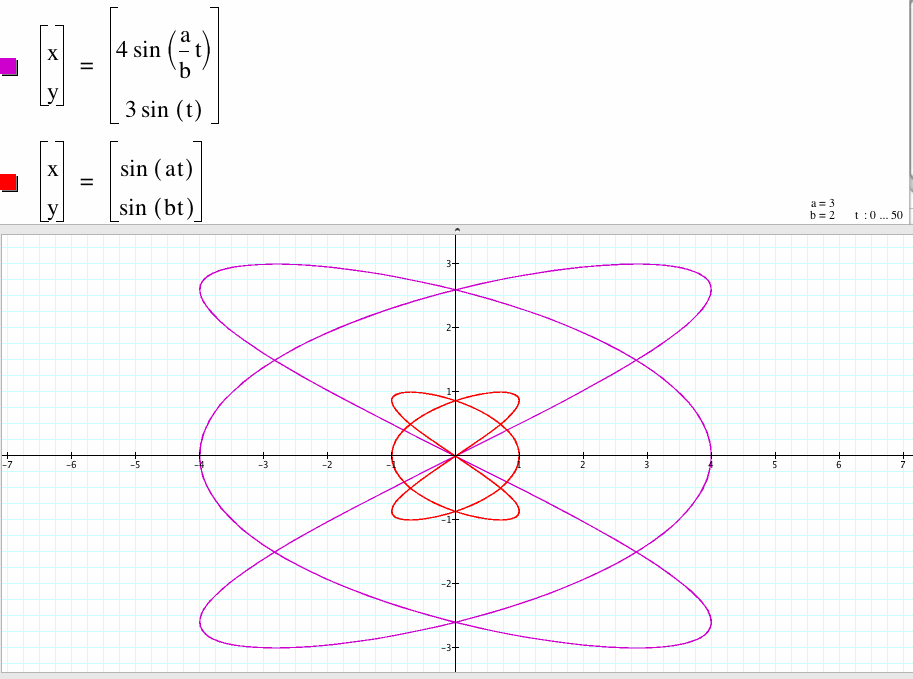
We generalize what we investigate. If the coefficient of the x coordinate is c, then the x-coordinate of the graph of the curve will range from -|c| to |c|. If the coefficient of the y coordinate is d, then the y-coordinate of the graph of the curve will range from -|d| to |d|.
Part Three
Course Evaluation