Suppose that one day, you were riding on your bike down the street and unfortunately a piece of gum got attached to your wheels. While the bike is still in motion, what will be the path of the piece of gum? Or suppose that you noticed a penny got stuck to the tires of your neighbor's car. While you are watching your neighbor's car drive out of the driveway, how will the path of the penny look like?
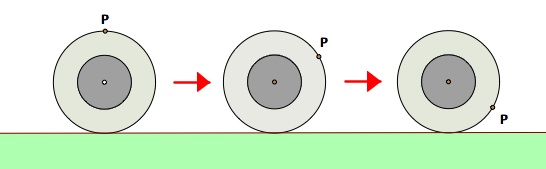
What is the path of the penny on a tire as the tire is rolled along?
In this writeup, we will like to examine the path of the penny that is stuck on a tire, as the tire is rolled along a level ground. That is, for a fixed point on a circle, we will like to investigate the path of the fixed point when the circle is rolled along, and come up with a mathematical equation for this path.
Let us use graphing programs to see how the path of the penny fixed on a tire looks like. Before we begin, what is your guess? Will the path look like repetitions of V-shaped line segments? Or, will the path look like repetition of circular loops (similar to captial gamma)?
To simulate a penny fixed on a tire, I have created a GSP file. Please click on this link to see the trace of the path: CLICK HERE The GSP file animates a penny fixed on a tire that is rolled along a level ground, and traces the path of the penny.
As it can be seen from the animation in the GSP file, the path of the penny looks like the following:
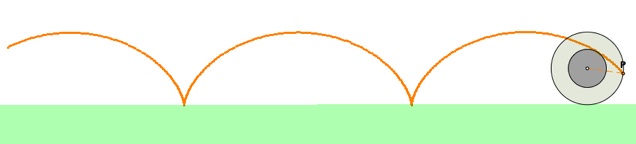
Tracing the path of the penny fixed on a tire
This path of the penny that is stucked onto a tire actually has a cool mathematical name: The Cycloid. In mathematical terms, the cycloid is the locus of a fixed point on a circle as the circle is rolled along a straigt line.
Now we will derive a mathematical equation of this path of the penny fixed onto a tire, or the cycloid. We will use parametric equations to derive this path of the cycloid, as it will be very convenient to do so.
First, let's set up a diagram that will help us understand the mathematical relationships. We need to examine the intial state and the after state of the fixed point, after the circle has rolled some distance. In the figure below, the left circle represents the initial state before the circle is rolled, and the right circle represents the after state.
Let us denote the fixed point on the circle as P and the radius of the circle as r. Let us assume that intially, the fixed point P is on the very top of the circle (12 o'clock position). Also, let us set up a x-y coordinate axis centered at the center of the intitial position of the circle as shown in the figure below.
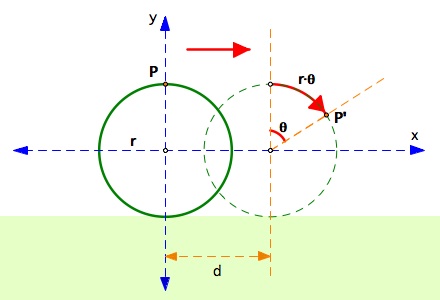
The intial and after state of the fixed point P as the circle is rolled a distance d
There is an important relationship between the distance the center of the circle has displaced (labelled as d) and the distance the fixed point P has moved along the arc, which is 
. Since the circle is in constant contact with the level ground, it follows that the distance d between the centers of the two circles must equal the distance point P has moved along the arc. That is,
** Notice that, we can express how far the tire has rolled by the central angle theta. For example, if the tire has rolled two complete revolutions, then it can be said that the tire has moved 720 degrees, instead of using distance measurements of feets or yards. **
Now, let us relate the central angle theta with the x and y coordinates of point P'. By constructing perpendicular lines from point P' to the x and y axis, we can construct a right triangle as highlighted by the orange lines in the figure below. Since the hypotenuse of the right triangle is radius r and one of the angles is theta, by using basic trignometry, the two sides of the triangle can be expressed as in the figure.
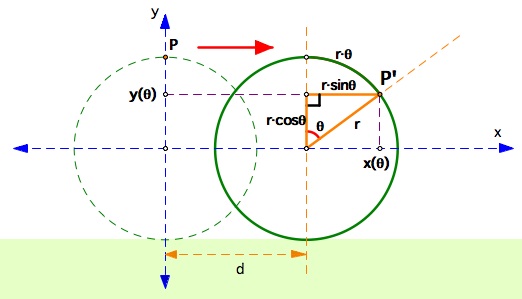
Relating the x and y coordinates of point P' to the central angle theta.
The x and y coordinates of the point P' can now be expressed from the center of origin of the x-y axis, which is the center point of the initial state of the circle. When the tire has rolled a central angle of theta, the x and y values are:
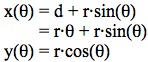
Therefore, the parametric equations of a fixed point on a circle as it is rolled, or the cycloid, is
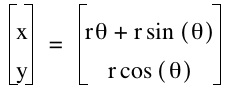
Let us check if this parametric equation will indeed give the desired shape of the cycloid. The graph of the equation with radius 1 looks like:
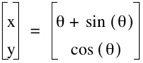
Graph of the parametric equation
Yes! This is the exact same path that we saw earlier.
Did you ever consider how would changing the velocity of the tire affect the path of the fixed point on the tire? This is a very good question to think about. Will different velocities of the circle give different paths of the cycloid? How about when the car is accelerating or decelerateing, that is when the velocity varies over time? Will this change the path of the fixed point on the tire?
Initially, I had the mistaken notion that if we double the velocity of the circle being rolled, then we would obtain a path with half the size of intervals. So I used d = v*t and graphed the parametric equations with twice the velocity. However, I found out that the graph is exactly the same!
This is because . . . no matter the velocity, it takes the same amount of revolutions of the circle to move a certain distance. A faster speed will result in the paths being drawn at a quicker rate, but the path will be the same, since the amount of distance required to move the circle one revolution is the same regardless of the speed. Notice that in our derivation, the parametric equations was not dependent on time.