

Valerie Russell
Assignment 10
Parametric Equations

Investigating parametric equations in the form x = a cos(t) and y = b sin(t).
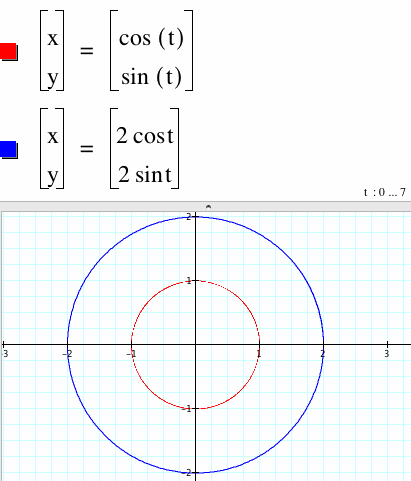 |
When a = b. Notice the parametrization of a circle of radius a or b. |
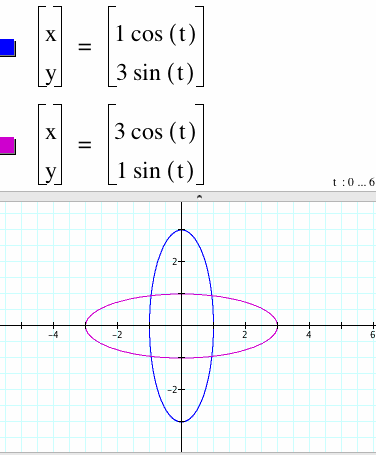 |
Parametric equations of the form: x = a cos(t) y = b sin(t) a < b: When a is less than b as in the first parametric equation, we no longer have a circle, An ellipse is formed whose major axis is vertical. a > b: When a is greater than b as in the second parametric equation, we also have an ellipse. The major axis is horizontal. It seems to appear that the values of a and b affect the direction of the major axis of an ellipse.
|
Let's investigate parametric equations for various values of a & b for x = cos (at) and y = sin (bt). We will let n represent these values.
x = cos(nt) y = sin(nt) Notice what happens when the coefficients of t are the same (a = b). The parametric equation still forms a circle but the radius does not change. |
|
x = cos(nt): -20 < n <20 y = sin(t) As the coefficient of t changes for cosine, the parametric equation forms an increasing vertical coil. Whether n is smaller than 1 or larger than 1, we still have the same vertical coil forming.
|
|
|
x = cos(t) y = sin(nt) -20 < n < 20 As the coefficient of t changes for sine, the parametric equation forms an increasing horizontal coil. The period I used here is 0 < t < 6.28. When b is zero, you have a horizontal line from -1 to 1. Whether n is smaller than 1 or greater than 1, the same horizontal coil is formed. |
RETURN TO HOME PAGE