

Valerie Russell


Exploring a
 |
|
Let's see what happens as a increases or decreases.
 |
As a increases the parabola stretches creating a narrower parabola |
 |
Likewise, as a decreases the parabola shrinks creating a broader parabola. |
So far we have seen that if the leading coefficient a is positive the quadratic function called a parabola opens upward and if the leading coefficient is negative the parabola opens downward. As a increases the parabola stretches and as a decreases the parabola shrinks.
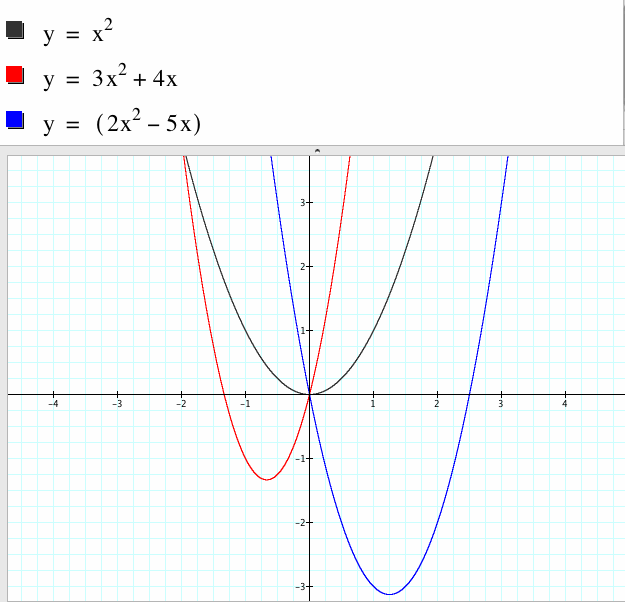
Exploring b
|
 |
|
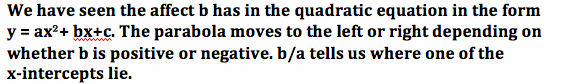
Exploring c
 |
Notice that as c increases the parabola moves upward. As c decreases the parabola moves downward.
|
![]()
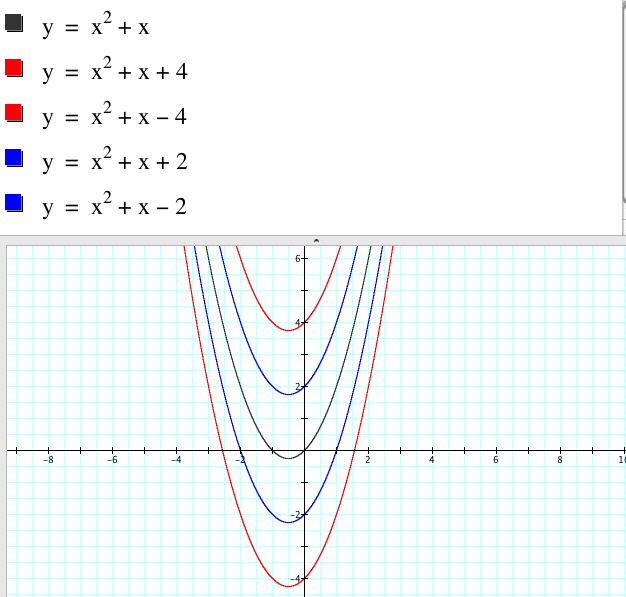
Did you know that you can easily see where the vertex and axis of symmetry lie in a quadratic equation when it is in vertex form? You can change the standard form of a quadratic equation to vertex form by using a method called completing the square. Let's take a look at several quadratic equations in vertex form.
 |
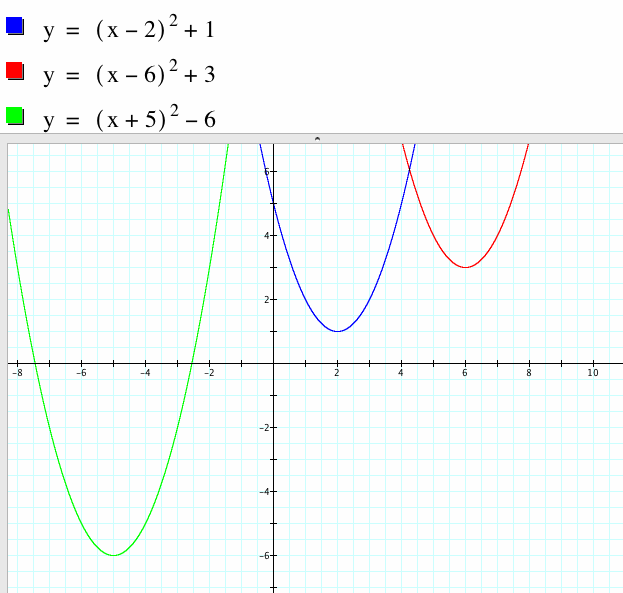 |
|
![]()
The coefficient of the quadratic equation a causes the parabola to shrink as a decreases and stretch vertically as a increases. |
|
Extensions:
![]()
Adding xy to the first equation allows us to see the parabolas in space. In both cases the parabolas are moved down 1 unit. |
RETURN TO HOME PAGE