

Assignment 2: Quadratic Equations
Ebru Ersari
Graph the parabola
i. Overlay a new graph replacing each x by (x - 4).
ii. Change the equation to move the vertex of the graph into the second quadrant.
iii. Change the equation to produce a graph concave down that shares the same vertex.
iv. Generalize . . .
First, let’s start to draw the graph of the parabola y = 2x² + 3x -4.
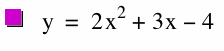

y = 2x² + 3x -4.
y = 2 (x² + 3/2x) - 4.
y = 2 (x² + 3/2x + 9/16) -4 -2( 9/16)
y = 2 (x² + 3/2x + 9/16) -( 41/8)
y = 2 (x+3/4)²-( 41/8)
The coordinate of the vertex of the parabola is (13/4, -41/8).
When I place (x-4) instead of x in the equation y = 2x² + 3x -4, the result is y = 2(x-4)² + 3(x-4) -4.
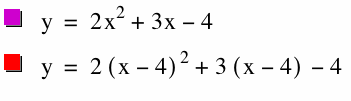

y = 2(x-4)² + 3(x-4) - 4
y = 2(x² - 8x +16) + 3x -12 - 4
y = 2x² - 16x +32+ 3x -16
y = 2x² - 13x +16
y = 2(x² - 13/2x +169/16)+16-2(169/16)
y = 2(x-13/4)²+16-(169/8)
y = 2(x-13/4)² -41/8
The coordinate of the vertex of the parabola is (13/4, -41/8).
When we compare the two coordinates of the vertexes of y = 2x² + 3x -4 and y = 2(x-4)² + 3(x-4) -4, the x coordinate moved 4 units to the right when we place x-4 instead of x in the equation, the y coordinate does not change.
ii. We should move the graph up to place the vertex in the second quadrant. Then, we need to change the constant.
When I add 4 to the equation, the graph moves up; however, it is still in the third quadrant. I need to move the graph up. Then, I add 4 to move the graph up, and the graph moves into the second quadrant.
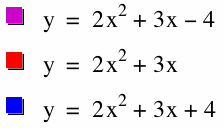
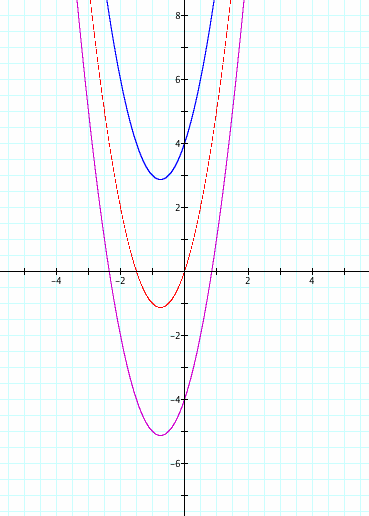
iii. To achieve a graph that is concave down and shares the same vertex as concave up graph, we should change the sigh of the x². When we draw y =-(2x² + 3x -4), we will achieve the concave down graph. The vertex of the graph is symmetric according to the x axis.
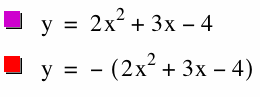
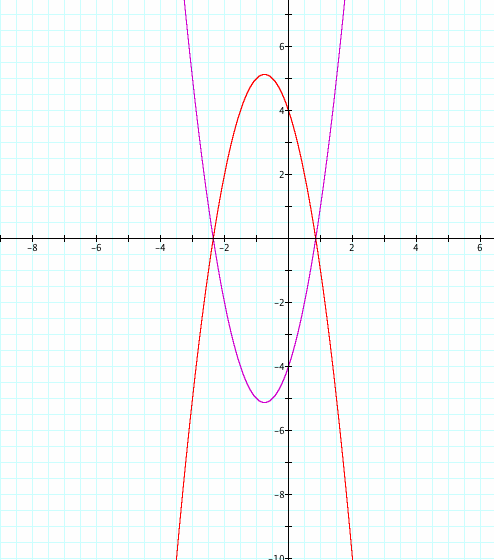
When we add as twice as the y coordinate of the vertex of y = 2x² + 3x -4, we will achieve the concave down graph that shares the same vertex because the vertexes of y =-(2x² + 3x -4) and y=2x² + 3x -4 are symmetric according to the x axis. We have already found the y coordinate of y = 2x² + 3x -4 as -41/8. Thus, we added 2(-41/8) to achieve the same vertex.
y=-(2x² + 3x -4)+2(-41/8) is concave down and shares the same vertex as y = 2x² + 3x -4.
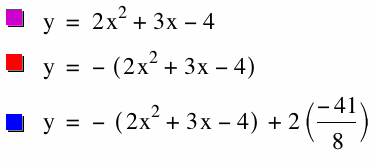
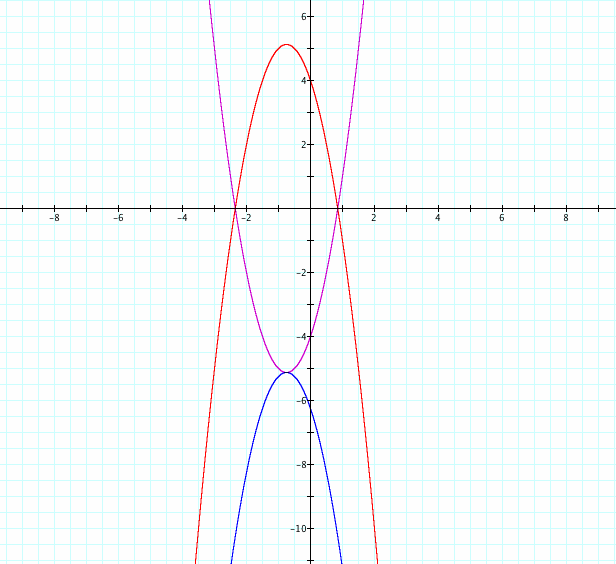
Generalization:
We can write the quadratic function y=ax²+bx+c as y=a(x - h)²+ k.
If a is positive, the graph opens upward, and if a is negative, the graph opens downward.
The coordinates of the vertex are (h, k), and when we change the h value, the graph will move right or left.
When we change the constant of the quadratic function, the graph will move up or down.
The negative sign of the function will give the reflected graph on the x axis. (in our example, y = 2x² + 3x -4 and y = -(2x² + 3x -4) are symmetric according to x axis).