

Jackson Huckaby
Now we want to discover how to find the center of the circumscribed sphere.
Let us begin by thinking about what we are looking for. We are starting with a tetrahedron and we wish to create a sphere that is going to surround this tetrahedron and only touch it at 4 points, the vertices.
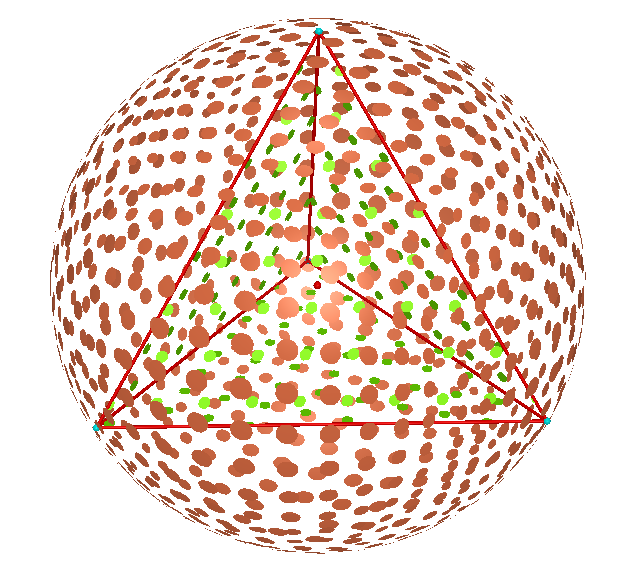
This is a multistep process, however it is not one which is beyond discovery. It will be important for students to think about the process we used in finding the circumcenter of the triangles in order to find the circumcircle.
This process is not much more complex, just in a third diminsional idea.
So we begin with the geometric definition of a sphere. A sphere is the set of all points in three diminsional space, which are equidistant from a point.
So, we know that if our sphere is going to be tangent to all four vertices of our tetrahedron, then there must be some point in space which is at the exact center of the 4 vertices of the tetrahedron.
Let's start with having the students open Cabri and construct a regular tetrahedron.
Now, we can go about the same process we used to construct the circumcircle.
| Circumcircle | |
|---|---|
1. Found all possible midpoints between Point A and Point B. 2. Found all possible midpoints between Point B and Point C. 3. Found all possible midpoints between Point A and Point C. 4.The intersection of these three lines gives us our circumcenter, constructing circle from this center to any vertex provides us with a circumcircle. |
So for step 1, we need to think of a way to locate all the possible points that are equidistant from two vertices. We know one point is at the midpoint of the edge that connects the two vertices, however this is obviously not our point. Since we are now thinking in three diminsions we have to bump up our set of points to be included in two diminsions. By constructing the perpindicular bisector of the edge between the vertices we find a plane that includes every possible point that is equidistant between two vertices.
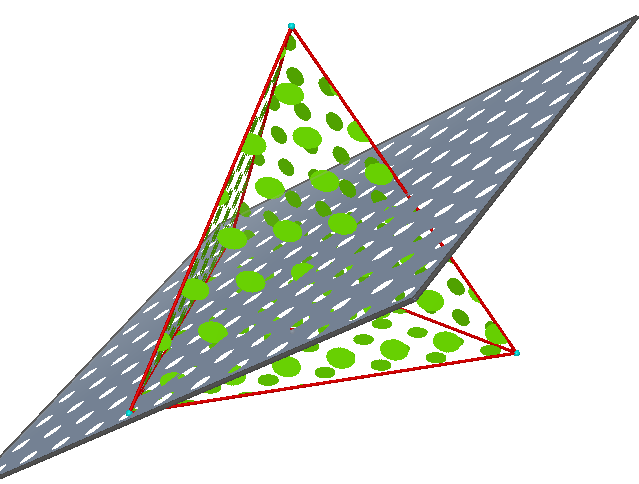
We see the result above. The gray plane bisects the edge of the tetrahedron. Next we repeat this process for 2 different vertices.
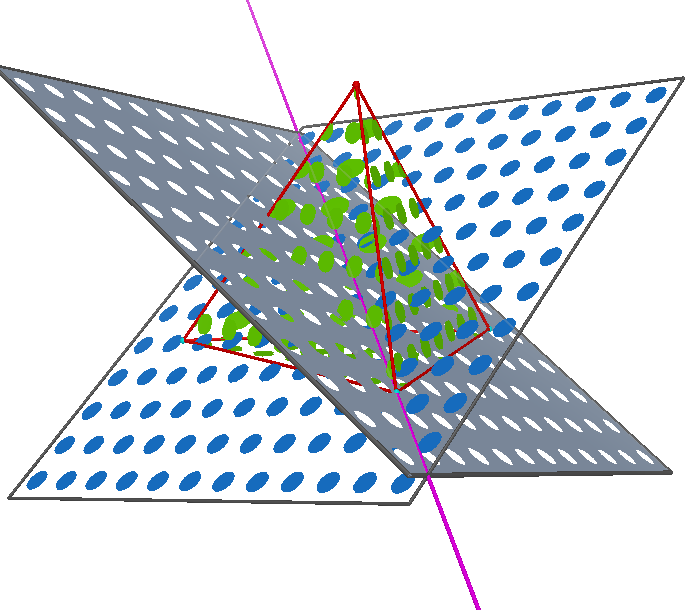
Now we have two planes including possible locations for the center of our circumsphere. We know that the desired point must lay on both of our planes, so our new possibilities include the intersection
of the planes. This line is seen in pink. We need 1 point however, so to finish our procedure we pick two more vertices and repeat the process one more time.
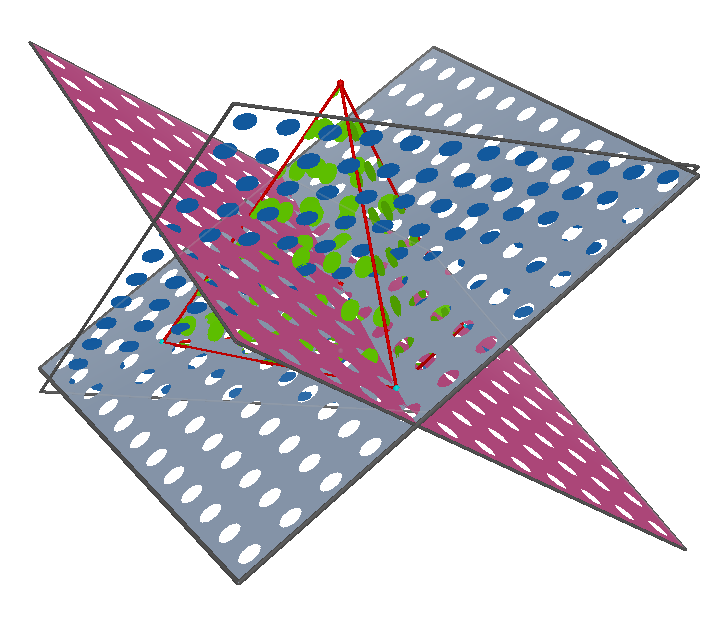
We have now inserted the maroon plane. We notice that our three planes do actually meet at one point, and we mark this point by a red dot at the center of our image.
According to our theory, we can now construct a sphere from this center point to any vertex on the tetrahedron and we will have a circumscribed sphere.
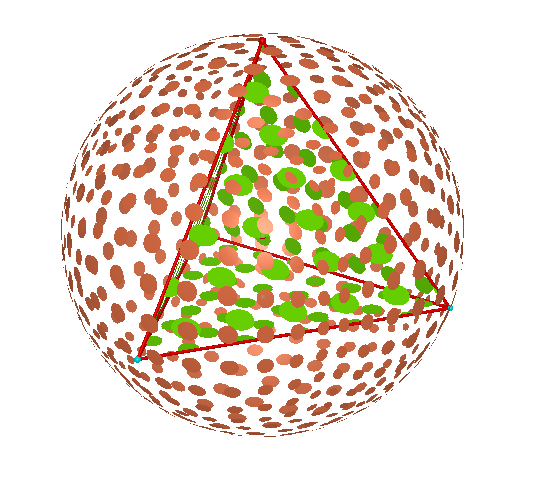
Congratulations.
Return home here.