

Final Project
by
Jackson Huckaby
Consider the graphs of the equation
xy=ax+by+c
for various substitutions of real number coefficients a, b, and c.
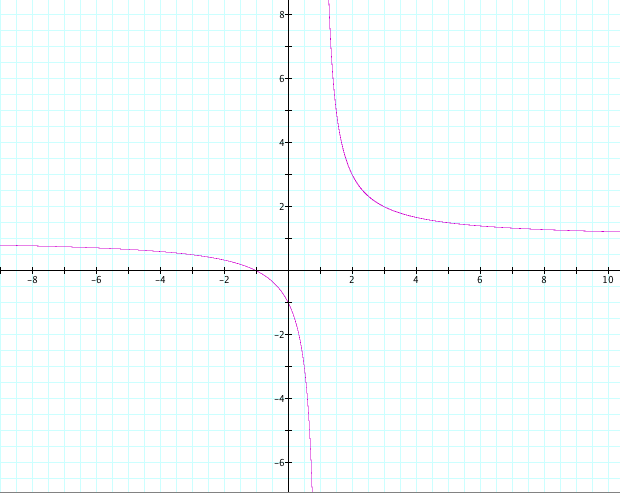
To explore this equation we will fix a and b, and create a slider value on c.
An interactive file can be found here.
As we set c equal to -2,-1,0,1,2,3 and overlay the graphs we get the following image.
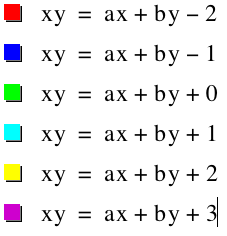
we see that the lines are pulling farther and farther away from the origin as n increases. We also see that when n becomes negative a reflection over the line x=1 occurs.
How else can we manipulate xy=ax+by+c?
Lets try setting x=0. So this becomes 0y=a0+by+c, or 0=y+c, using the same values of c we get the following set of horizontal lines:
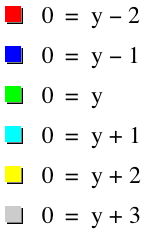
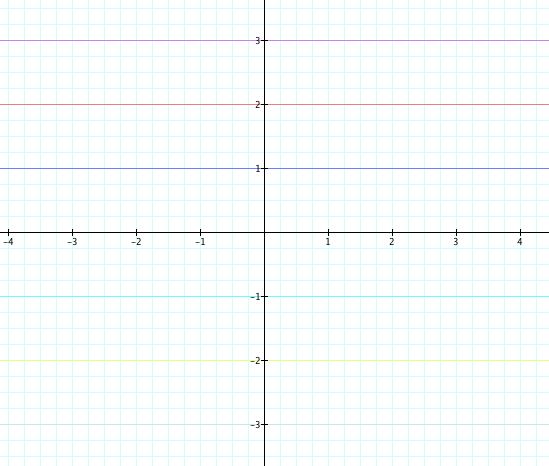
If we make y=0 instead of x, we get 0=x+c. This will result in a set of vertical lines.
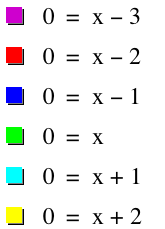
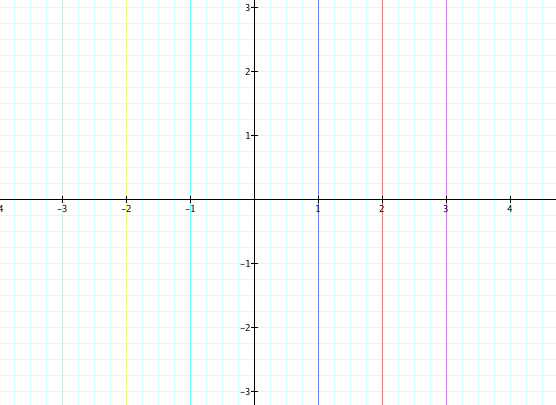
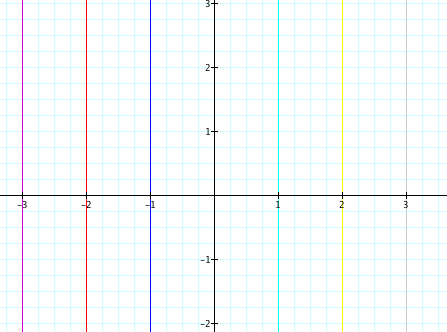
Lets observe the graphs of x-b=0 and y-a=0
Rewriting x-b=0 first, we get x=b.
So therefore by setting b equal to -3,-2,-1,0,1,2,3 we get:
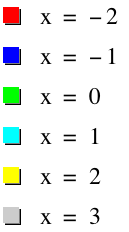
Lets try the same thing with y=a, we can predict that this time we will get vertical lines instead.
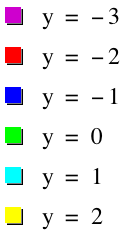
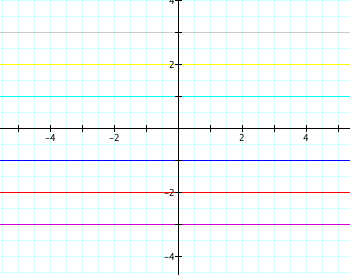
And we do!
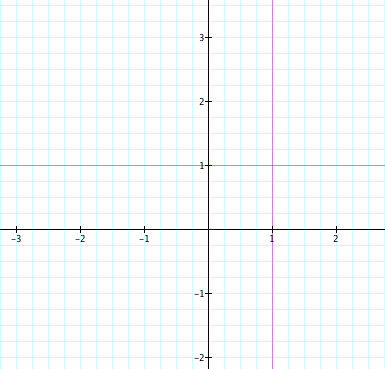
So now let us explore the affect of graphing (x-b)(y-a)=0
And then let us graph our original equation xy=ax+by+c on the same plane:
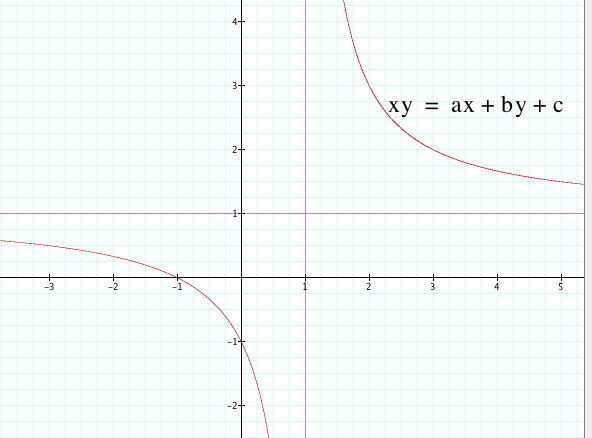
So let us vary our c values and overlay again and see what we get:
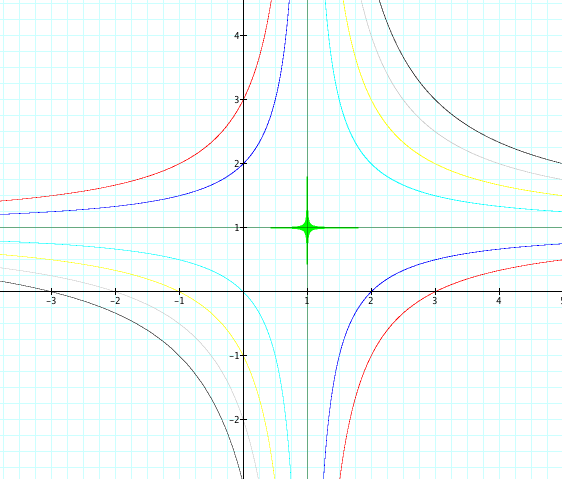
By looking at this graph we can clearly see that the graph of (x-a)(x-b)=0 gives us our asymptotes for the equation xy=ax+by+c.
So let us examine why this could be true. If we distribute:
(x-b)(y-a)=n(for any n)
xy-ax-by+ab=n
xy=ax+by-ab+n
And compare this to our equation in question: xy=ax+by+c
So: as long as c=-ab+n then we are getting the same equation.
Lets verify.
If we let a=5 and b=-2 and n=1
(x+2)(y-5)=1
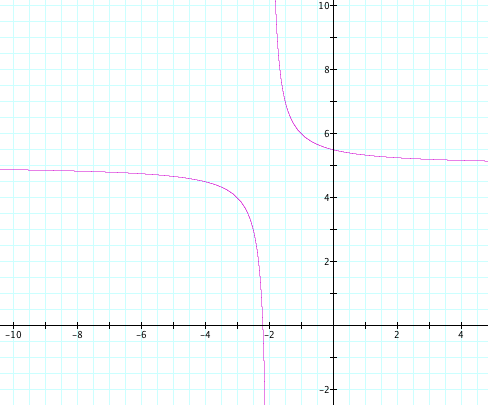
And then let us graph xy=5x-2y+11:
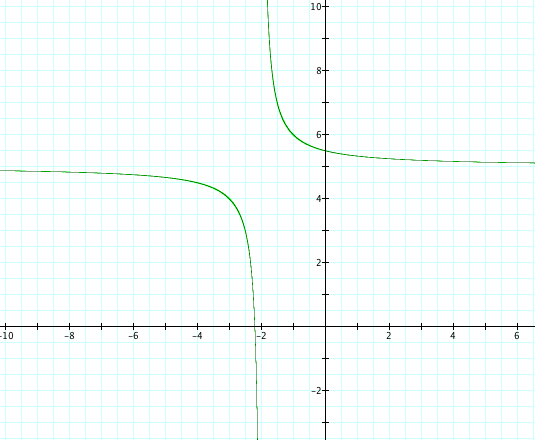
And what we realize is...


They are the exact same graph!
Return to final page.