We have seen that the triangular numbers are formed by the following sequence:

1, 3, 6, 10, 15, 21, …

We can also represent these in tabular form. We’ll call the first triangular T(1), the second triangular number T(2), and so forth.

n	T(n)
1	1
2	3
3	6
4	10
5	15
6	21

If we investigate the finite differences for the T(n) column, we’ll find that the second order differences are constant:

n	T(n)	1^st Differences	2^nd Differences
1	1
2	3	2
3	6	3	1
4	10	4	1
5	15	5	1
6	21	6	1

So how is this useful information to us? Well, it allows to model T(n) as a quadratic function (since the second-order differences are constant).

In other words, T(n) may be expressed in the form an² + bn + c, for some appropriate values of a, b, and c.

So T(n) = an² + bn + c

This implies the following (by substituting the ordered pairs from the table above):

T(1) = a + b + c = 1

T(2) = 4a + 2b + c = 3

T(3) = 9a + 3b + c = 6

We could use any three of the ordered pairs in the table. Three pairs are sufficient and necessary, because three equations would allow us to solve for three unknowns. Normally one chooses the lower ordered pairs for the sake of convenience, but it is up to the individual to make the decision.

From here, we recommend the use of a graphing calculator with the ability to row-reduce a matrix. For our demonstrations, we are using the TI84 + Silver Edition.

For those not familiar with matrix operations on the TI84 calculator, we will demonstrate each part of the process.

First, create a matrix with the coefficients of a, b, and c, as well as the T(n) valued associated a, b, and c in each equation above. The matrix we will create will be the following matrix: .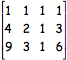

Press [2^nd] [x^-1] to access the Matrix menu and arrow to the right so that EDIT is highlighted. Select “1:[A]”. Now we’ll edit Matrix A so that it becomes the matrix above.

Type in the dimensions of the matrix A as 3x4. Next, input the entries into the matrix. We’ll solve this system of equations for a, b, and c by row-reducing matrix A (in Reduced Echelon Form).

After you have entered the entries for A, quit the matrix menu (by pressing [2^nd] [MODE] to quit).

It is a good practice to view your matrix on the home calculator screen in order to verify that it has been entered correctly. Access the matrix menu as we did above. With the NAMES menu highlighted, select matrix A by pressing [1] and then press enter.

This looks like it is supposed to look, so we will proceed. Select the matrix menu again. Choose [MATH] and arrow down to the rref( option. Select that one by pressing enter.

Now go back to the matrix menu (NAMES) and choose Matrix A.

Now press enter:

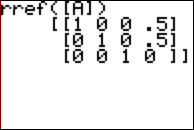
So we can see by matrix operations that a = 0.5, b = 0.5, and c = 0, which implies the following:

T(n) = 0.5n² + 0.5n + 0 è .

So now we have found a formula for representing the nth triangular number.