Quadratics in the XC plane
by Kasey Nored
Our parent quadratic makes our
familiar parabola.
y = ax2 + bx + c where b and c equal zero
The manipulation of a, b, and c
shifts and dilates our parabola.
This write-up intends to explore
the xc plane where c serves
as y, for example to graph a point in the xc plane
(x, c) would be the coordinates. When we manipulate our quadratic ax2 +
bx + c, using 1 for a and b, and solve for c we find
that c = –x2 – x
Our xc plane appears to merely flip and shift our parent
function, with our vertex at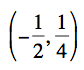
When we change our original value
of c to 5, the red graph, or to .25, the black graph, our parabola dilates but
also moves our vertex.
For the equation
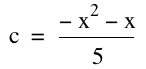our vertex lies at
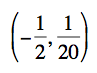and the graph still has zeros at 0 and -1 which is reasonable
as our zeros are linked
with our values of a and b and here we have not changed our a and b values.
For the equation
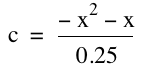our zeros remain and our vertex lies at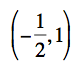 
If we animate the denominator for
values between -10 and 10 we see the graph below.
You notice that the graph
continues to have the original zeros and dilates while changing the vertex.
Also of interest is the point
where c = 0 the graph is undefined.
Return to EMAT 6680
Return to my page