

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
In Assignment #2, we did a exploration of the quadratic equation:
![]()
We looked at the changes in the graph as we varied a while b and c remained constant. Also, we looked at when c was varied while a and b remained constant.
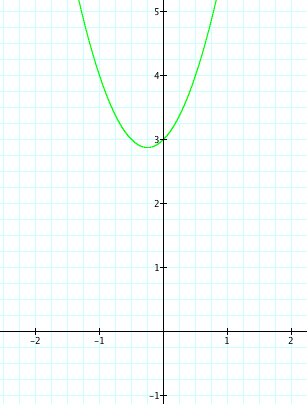
Now, let's look a little closer at the graphs when the values of a and c are constant and b is varied. As in Assignment #2, lets look at when a=2, c=3, and b is varied.
![]()
No matter the value of a, this parabola still passed through (0,3), as we discussed in Assignment #2. Will this be true when b is varied? When x=0, then y will still be 3 so therefore, it seems to reason that this will also be true for any value of b. Let's begin to look at our graphs when b varies from 4 to -4 and see if our assumption is correct.
 |
 |
 |
 |
 |
|||
 |
 |
 |
 |
Again, each parabola passes through the point (0,3). This should come as no surprise. When x=0, then our a and b also become zero, leaving y to equal the value of c.
Now, let's look at graphs in the xb plane.
Let's again consider the equation:
![]()
If we set:
![]()
and then solve for b we get the following graph in our xb plane:
 |
 |
Now, lets also graph b=7:
 |
 |
Let's think about roots.Watch the animation below and we will see our value of b move from 10 to -10.
We know that we can find how many roots, if we consider the discriminent.
| Discriminent = |
| If our discriminent is less than 0, there are no real roots. | ||
| If our discriminent is equal to 0, there is one real roots. | ||
| If our discriminent is greater than 0, there are two real roots. |
In our case, a=2 and c=3, so we can find our roots by solving the discriminent.
We can see that b has two negative real roots when b>4.89898, one negative real root when b=4.89898, one postive real root when b=-4.89898 and two postive real roots when b<-4.89898. When -4.89898<b<4.89898, there are no real roots. We can see that if our value of c changes but c>0, that b will still have the same roots just at a different value.
Now, consider the graph when our c=-3:
 |
 |
This shows us that there are two real roots when b=7. What will happen when b is varied? Watch the animation below to see.
Reguardless of the value of c, if c<0 we will have 2 real roots for b.
Depending on the value of b, we either have two real roots, one real root, or no real roots. This again can be determined by the discriminent. Take when c = 0:
Then roots are found when x = 0 or x = -b. When b is a value, there are two real roots. However, when b = 0, then there are two roots at zero.
When c<0, there are always two real roots. Again this can be checked by using the discriminent.
Conclusion
1) When c>0: Depending on the value of b, there are two negative real roots, one negative real root, one postive real root and two postive real roots, or there are no real roots. This can be checked by using solving for the discriminent.
2) When c<0: Reguardless of the value of c, if c<0 we will have 2 real roots for b.
3) When c=0: There are two real roots.