

Kate Berryman
cavaleri@uga.edu
*Please make sure your browser is maxiumized to view this write up;
Prove that the lines of the three altitudes of a triangle are concurrent.
Proof:
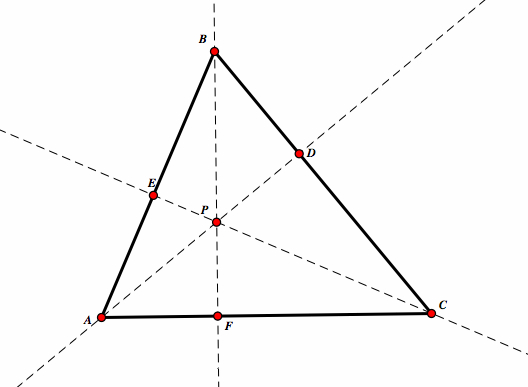
Take any triangle ABC. Construct a perpendicular line passing through A and perpendicular to BC, through B and perpendicular to AC, and through C and perpendicular to AB. Label these intesections D, E, F respectively.
Now, we must prove that AD, BF, and CE are concurrent at point P.
Next, construct a line passing through A parallel to BC, a line passing through B parallel to AC, and a line passing through C and parallel AC.
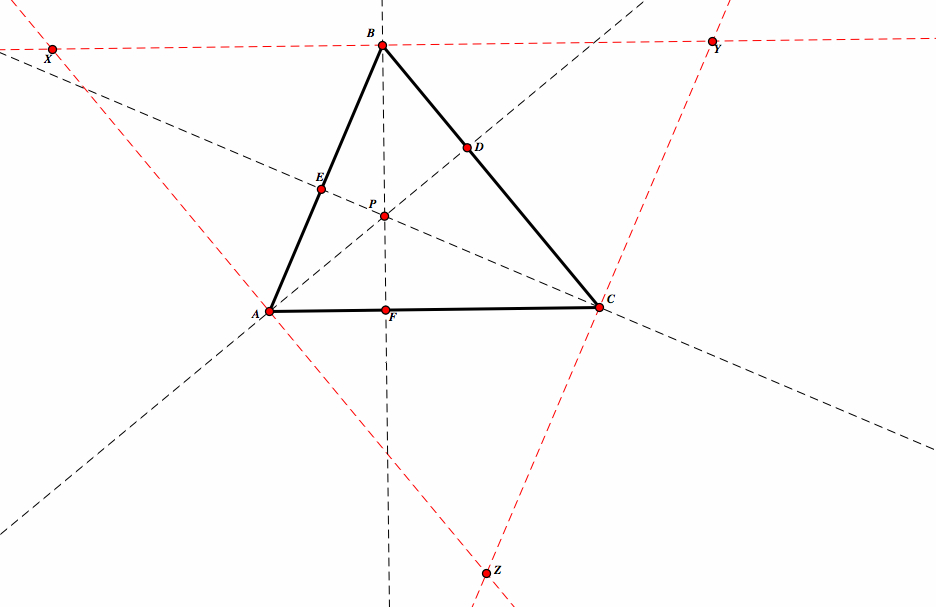
Now, look at parallelogram XBCA. We know that AC=XB. Also, if we look at parallelogram PYAC, then BY=AC. Therefore, BY=XB. Since BY=XB, then B is the midpoint of XY. Similiarly, if we look at parallelogram ACBX, AX=CB and CB=AZ. Therefore AZ=AX, so X is the midpoint of XZ. Lastly, if we look at parallelogram ABCZ, CZ=AB and AB=CY, therefore CZ=CY so C is the midpoint of YZ.
So points A, B, and C are the midpoints of the sides of triangle XYZ. Since AD, CE, and BF are perpendicular to the sides of XYZ, then it follows that they are concurrent at point P.