

Assignment 3:
Exploring the Graphs of the Equations x2 + bx + c = 0 in the Plane xb for Various Values of c
by
Ángel M. Carreras Jusino
Goal:
- Find a relationship between the graphs of the equations of the form x2 + bx + c = 0 in the plane xb for various values of c and the number and types of roots of such equations.
Consider the graph of the equation x2 + bx + 1 = 0 in the plane xb.
If we overlay the graph of b = constant to the graph above, their intersections are the roots of the equation x2 + bx + 1 = 0.
Example for b = -4
Note that for |b| = 2 there is one real solution, |b| > 2 there are two real solutions, and for |b| < 2 there is no real solution. See the following animation.
Now lets explore the graphs of the equations of the form x2 + bx + c = 0 in the plane xb for various values of c.
From the animation above can be noticed that:
Let explore each case.
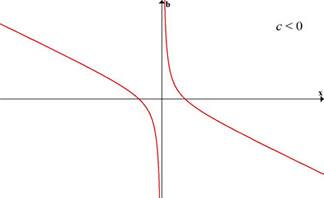
Case 1. c < 0
When c < 0, we always have two real roots no matter what is the value of b.
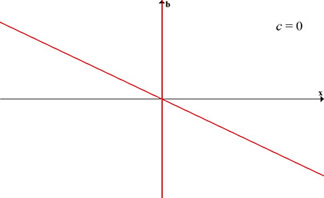
Case 2. c = 0
When c = 0, according to this graph the equation has only one real root for any value of b, specifically the solution x = -b.
But if we look to the equation x2 + bx + c = 0 with c = 0,
x2 + bx = 0
x (x + b) = 0
x = 0 and x + b = 0
x = 0 and x = -b
Now, why the solution x = 0 doesn't appear in the graph?
This happen because what is graph in the graphing software was an algebraic manipulation of the original equation which exclude 0 from its domain.
x2 + bx = 0
bx = -x2
b = -x2⁄x where x ≠ 0
b = -x
Therefore for c = 0, we always have two real roots x = 0 and x = -b.
Case 3. c > 0
Here for different values of b we have 0, 1, or 2 real roots for the equation.
Now lets explore for which values of b we have the different number of real roots.
Looking at the animation we can note that the equation have one real root when the graph of the equations x2 + bx + c = 0 for c > 0 in the xb plane have slope 0.
Differentiating.
Equating to zero.
Evaluating the equation in this values of x we get:
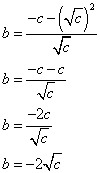
So when c > 0 the equation x2 + bx + c = 0 has:
no real solution if b < |2√c|
one real solution if b = |2√c|
two real solution if b > |2√c|
Note that this is equivalent to the discriminant b2 - 4ac, which gave us information about the number and type of solutions of a quadratic equation.