Assignment 8:

Altitudes and Orthocenters

by

Ángel M. Carreras Jusino

Goal:

Given a triangle ABC, construct the orthocenter H. Let the points D, E, and F be the feet of the perpendiculars from A, B, and C respectively. Show that:

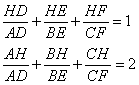
Exploration

In the following applet is shown

Drag the point A and see what happens to H. Investigate what happen when A is inside, outside, and on the circle; and inside, outside, and on the parallel lines. Also, check how the results of the two formulas vary as you move A.

Sorry, this page requires a Java-compatible web browser.

You should note that:

  • When A is in the circle or outside the parallel lines, the triangle is obtuse and H lies outside of it.
  • When A is in the interior of the parallel lines and outside the circle, the triangle is acute and H lies inside of it.
  • When A is in the circle or in one of the parallel lines, the triangle is right and H lies on it, specifically in one of its vertices.
  • The results of the two formulas are constant (1 and 2 respectively) when the triangle is acute, i.e., H is inside the triangle.

Case 1. ABC is an obtuse triangle.

If ABC is an obtuse triangle, then the orthocenter is outside the triangle.

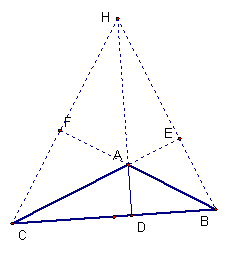
Note that in the case of an obtuse triangle most of the following ratios are greater than 1.

In the diagram presented is clear that the ratios

are greater than 1.

Therefore for an obtuse triangle

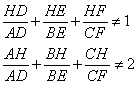
Case 2. ABC is an acute triangle.

Let consider the following figure to see if the given formulas are true for all acute triangles.

Remember from the Exploration that to have an acute triangle (and as a result have H inside the triangle), A must be in the interior of the two lines perpendicular to BC at B and C, and outside the circle with diameter BC. In terms of the figure above these can be summarized by the following expressions.

(1)

(2)

We only consider the upper hemisphere of the circle in this case.

Note that the expression inside the radical is always positive because of (1).

*These facts [(1) and (2)], in addition to the two which are presented below, will be constantly used during the proof.*

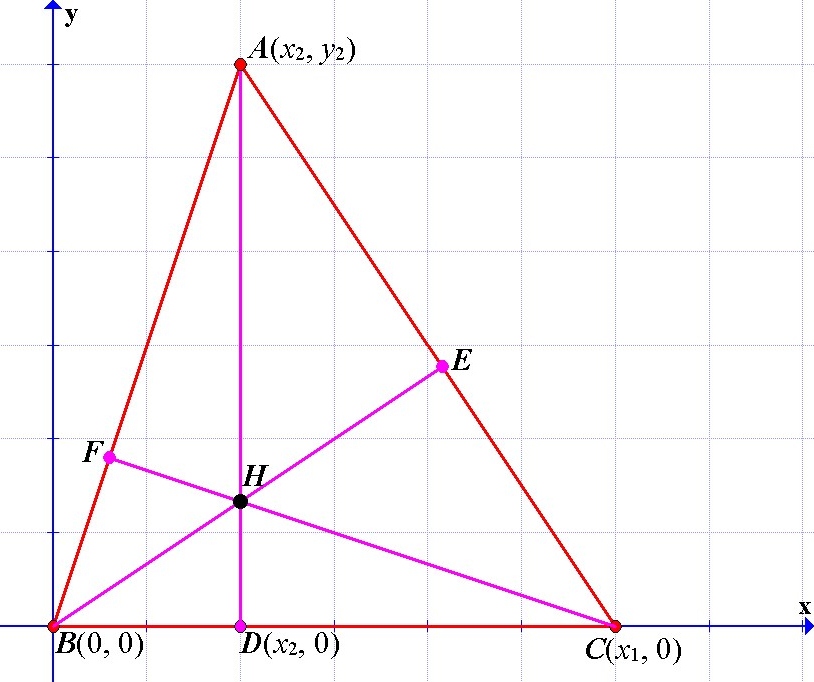
Now, we are going to find expressions for the distances required to prove the formulas algebraically.

Note that

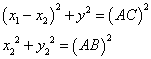
First, let find the coordinates of the points H, E, and F

We already know the equation of the altitude that goes through the vertex A

So if we find the equation of another altitude, we can find the coordinates of the orthocenter (H).

Let work with the altitude from B to the line containing the segment AC. The slope of the segment AC is given by

Now the slope of the altitude is given by

Because the altitude contains the origin, the equation of the altitude is

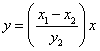
Now we find the interception of the altitudes

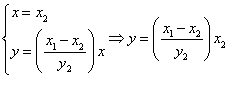
Therefore the orthocenter has coordinates

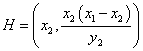
To find the coordinates of E, we need to find the interception of the altitude from B to the line containing the segment AC and the segment AC. We already determined the equation for the altitude

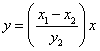
Let look for the equation of the line containing AC. The slope of this line is given by

This line contains the point C, using the point-slope form we get

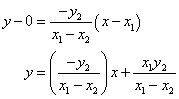
To find E we solve the following system

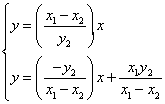
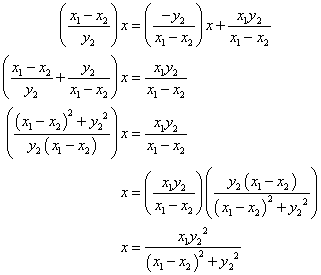
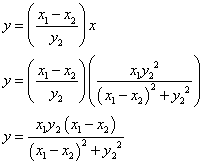
Therefore E has coordinates

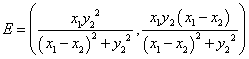
Similarly, F has coordinates

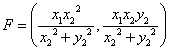
Now, let calculate the distances needed to prove the identities.

 

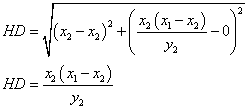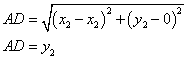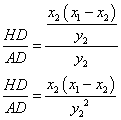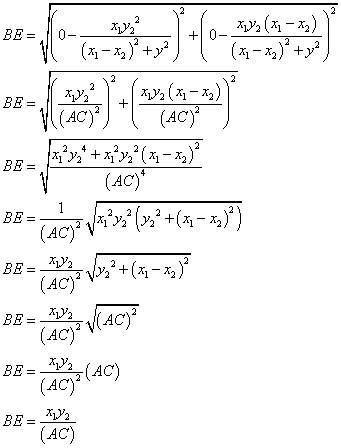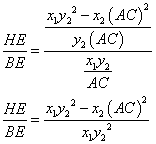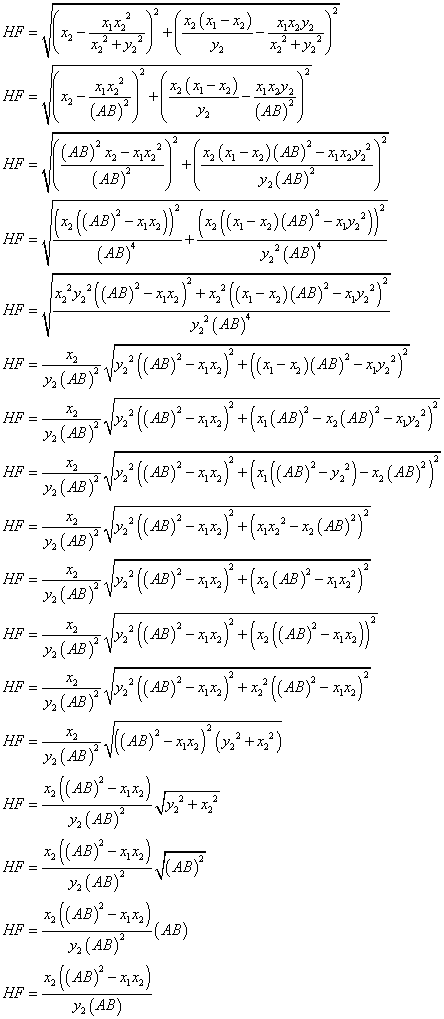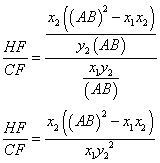Now, let check the first identity

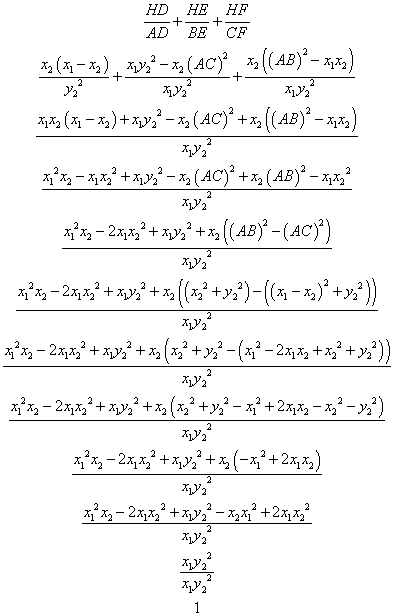
To check the second identity we need to find AH, BH, and CH.

 

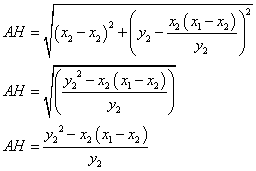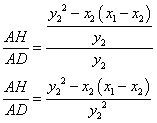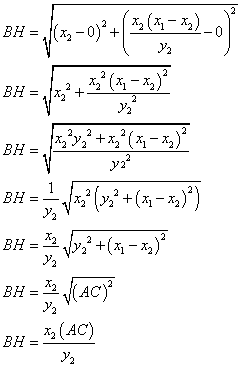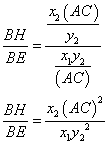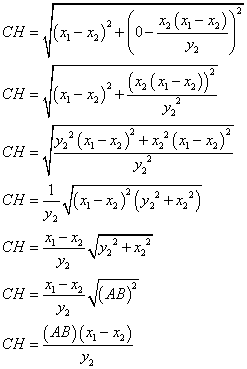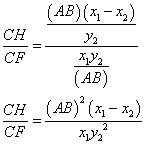Now, let check the second identity.

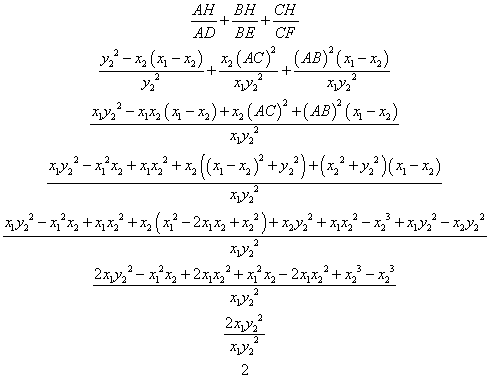
Case 3. ABC is a right triangle

Let consider the following figure.

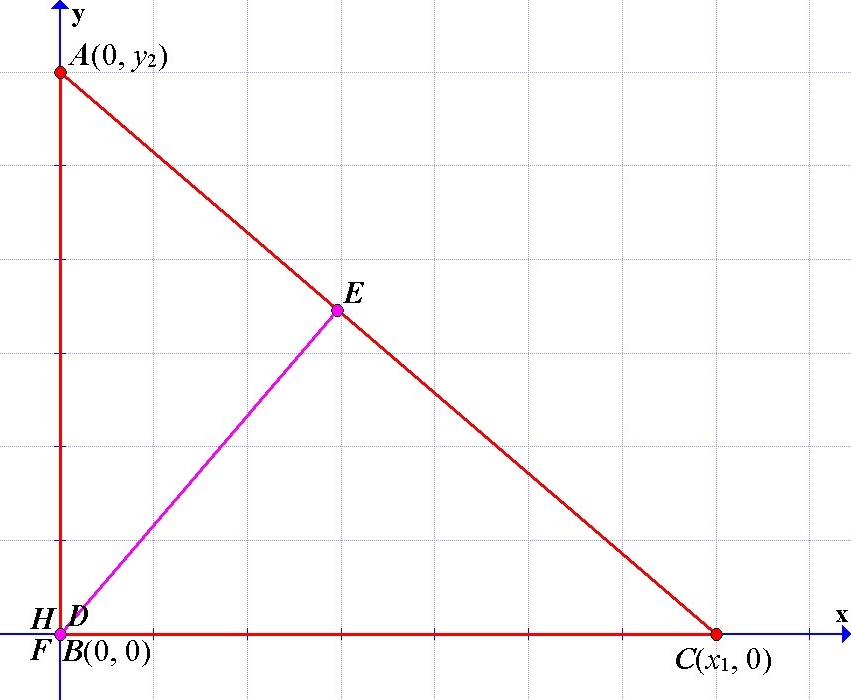
Is clear that the altitudes from the perpendiculars from A and C coincide in B, therefore D, F, and H lie in the origin.

Now let find the coordinates of the point E. This point lies in the intersection of the line AC and the altitude that goes through the vertex B

First, the slope of the line AC is given by , therefore its equation is .

Because BE is perpendicular to AC its slope is , therefore its equation is .

Solving the system we can find the coordinates of E.

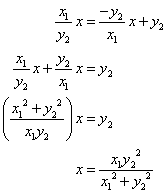
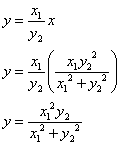
E has coordinates .

Now, having all the coordinates of the points let proceed with finding the distances required to check the formulas.

.

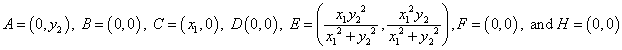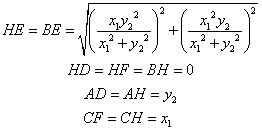
Finally,

After the examination of these three cases we can conclude that given a triangle ABC, with orthocenter H, and the points D, E, and F the feet of the perpendiculars from A, B, and C respectively then if the triangle ABC is not obtuse.

Return to Angel's Homepage

Return to EMAT 6880 Page