In this write up , we will be investigating tangent cricles and their constructions.

In order to construct a circle tangent to two given circles one will need to follow the steps below.

Construct a circle with center O1 and another circle with center O2.

Construct lines l1 and l2 that pass through O1 and O2 respectively.

Select a point of tangency P on circle 1 and use such a point as the center of a circle Identical to Circle 2. Let C3 be the center of this circle.

Construct a line segment that joins C2 and C3 and make this the base of a isoceles triangle.

The next step is to construct a perpendicular bisector to C2C3. The center of our Tangent circle will lie on the perpendicular bisector.

Feel free to use the sricpt tool below by dragging points to construct a tangent circle to two given circles.

Enjoy !!!.

Tangent Circle Srcipt Tool.

There Are Three cases:

Case1: One circle inside the other one.

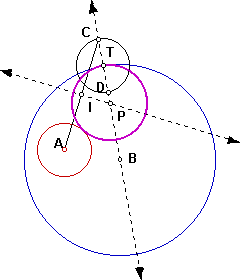
An investigation using GSP suggest that we have a circle as the locus.

Case 2: The circles are disjoint.

An investigation of our GSP animation suggest that the locus is an hyperbola as picture above.

Case 3: The circles Intersect.

An investigation of our GSP construction suggest the locus is an ellipse.

Return to Home Page.