Assignment #2
Explorations in the Shifts
of Parabolas
by
Kimberly Burrell
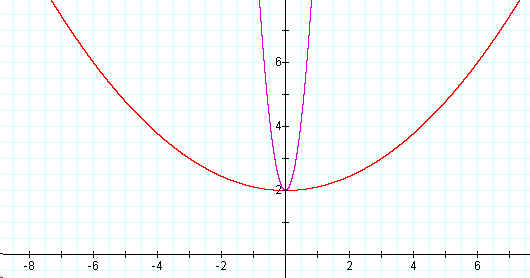
The following will be an exploration involving both horizontal and vertical shifts of a parabola given by the equation
![]() .
.
The following explorations were prepared on the Graphing Calculator software by Pacifictech.
HORIZONTAL SHIFTS
In order for the parabola to shift directions horizontally, one must change the values of d in the equation
![]() .
.
In this equation the vertex is denoted by (d, -2).
The graph below illustrates the type of shift that occurs when d = 1, d = 2, d = 4, and d = 6.
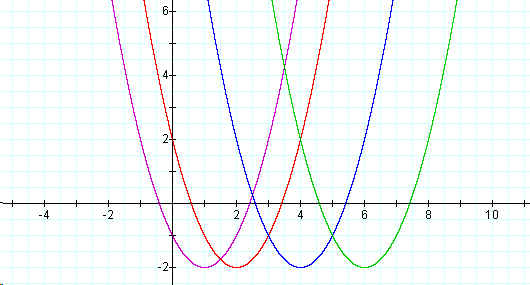
From this graph, one can observe that a positive value of d will result in a horizontal shift to the right by the number of units, d.
The next graph demonstrates the type of shift that occurs when d = -1, d = -2, d = -4, and d= -6.
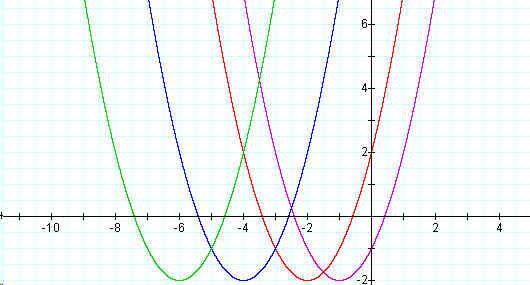
One can observe from the above investigation that a negative value of d will result in the graph shifting horizontally to the left, d units.
VERTICAL SHIFTS
In order for the parabola to be shifted vertically, one must change the values of k in the equation
![]() .
.
In this form the vertex is (d, k). While performing this exploration d will remain zero.
The graph below illustrates the type of shift that occurs when d = 2, d = 3, d =5, and d = 7.
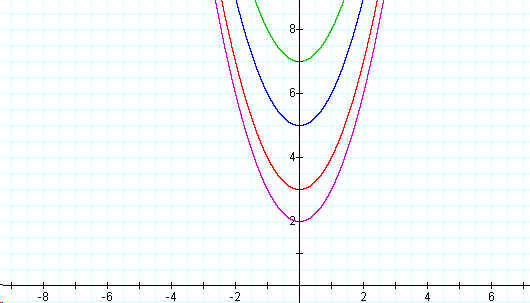
From this graph, one can observe that a positive value of k will result in a vertical shift upward by k units.
The next graph demonstrates the type of shift that occurs when d = -2, d = -3, d = -5, and d=-7.
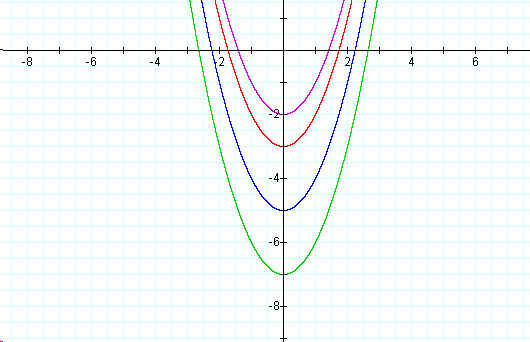
One can observe from this investigation that a negative value of k will result in a vertical shift downward by k units.
CONCLUSION
By changing the values of d, the parabola will be shifted horizontally by d units. This shift will be to the right if d is a positive number or to the left if d is a neagtive number.
By changing the values of k, the parabola will be shifted vertically by k units. This shift will be in the upward direction if k is a positive number and in the downward direction if k is a negative number.
These changes do not effect the shape of the parabola.
EXTENSION
In order to change the shape of the parabola one must change the coefficient of x.
An integer coefficient of x will make the parabola to become narrow or stretch. A rational coefficient, which is not an integer, of x will make the parabola become wider or shrink.