

Assignemnt #4
Orthocenter of a Triangle
by
Kimberly Burrell
The orthocenter of a triangle is located at the intersection of the altitudes of the sides of the triangles.
It is intersecting to examine the location of the orthocenter for different classifications of triangles.
ACUTE TRIANGLES
Acute Isosceles

In this instance, the orthocenter is located in the interior of triangle.
Acute Scalene
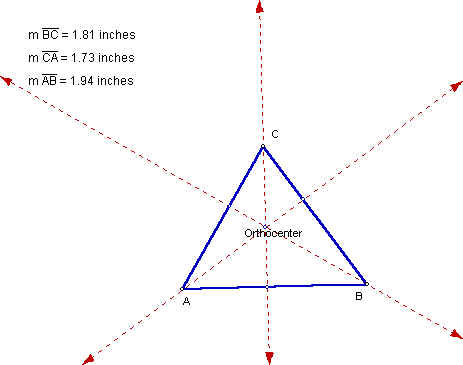
Again, the orthocenter is located in the interior of the given triangle.
Acute Equilateral

In this final classification of acute triangles, we again find that the orthocenter is inside the triangle. To explore, click here.
CONCLUSION: The orthocenter of any acute triangle is located in the interior of the triangles.
RIGHT TRIANGLES
Right Isosceles
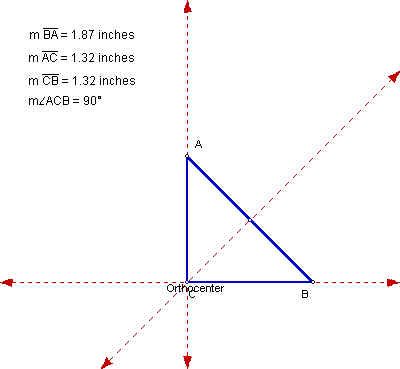
In this instance, we see that the orthocenter is located at the vertex C, opposite the hypotenuse of the right triangle.
Right Scalene
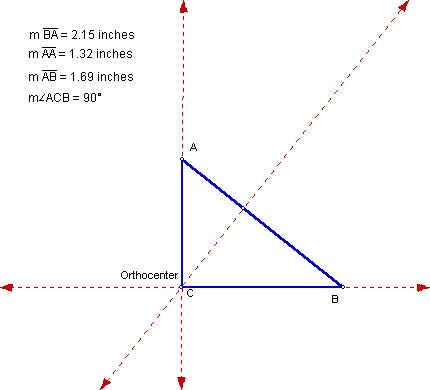
Again, we find that the orthocenter is located at the vertex C, opposite the hypotenuse of the right triangle.
CONCLUSION: The orthocenter of a right triangle is located at the vertex C, opposite the hypotenuse of the right triangle.
OBTUSE TRIANGLES
Obtuse Scalene
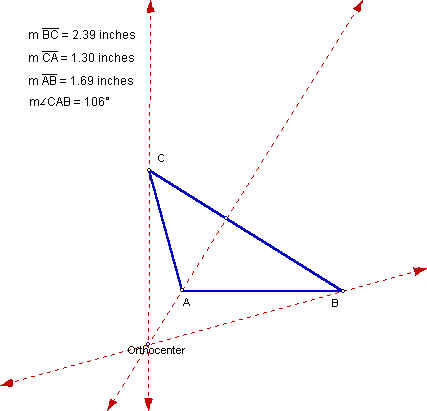
In this case, we see that the orthocenter is located outside of the given triangle. Also, notice that it is opposite the longest side and behind the obtuse angle.
Obtuse Isosceles
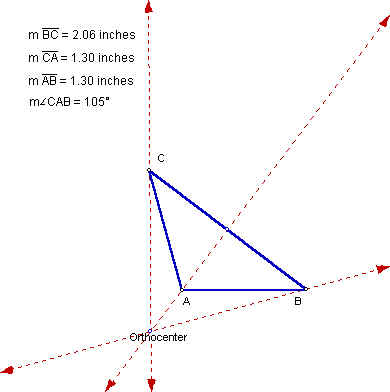
We find the same situation in this instance. The orthocenter is outside the triangle, opposite the longest side, and behind the obtuse angle.
CONCLUSION: The orthocenter of an obtuse triangle is located outside the triangle, opposite the longest side, and behind the obtuse angle.