

Investigations with the Pedal
Triangle
by
Kimberly Burrell
The pedal triangle, RST, is formed by choosing any arbitrary point and any arbitrary triangle. The arbitrary point P is known as the pedal point. In this investigation the arbitrary triangle will be triangle ABC. The pedal triangle is formed from the perpendiculars to the sides of triangle ABC to locate the three intersection points, R, S, and T. The following is an example of a GSP sketch of a pedal triangle.

In the following we will look at various pedal triangles that have been constructed by allowing the pedal point to be specific points related to triangle ABC. We will also explore other characteristics of the pedal triangle by use of animation with GSP.
Click here for a GSP script of the pedal triangle construction.
Now let's allow the pedal point to be located at the incenter, the point inside of the triangle that is equidistant from all the sides of triangle ABC.
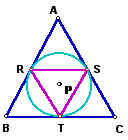
The pedal triangle is located in the incircle of triangle ABC. The incircle goes through the points of intersection of the lines through the incenter and perpendicular to each side of triangle ABC. As one can observe, the incircle of triangle ABC is actually the circumcircle of the pedal triangle RST.
Now, lets allow the pedal point to be the circumcenter, the intersection point of the perpendicular bisectors of triangle ABC.
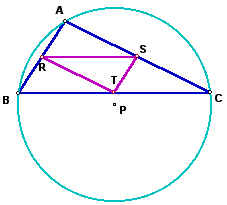
With the circumcenter being the pedal point, the midpoints of triangle ABC become the vertices of the peadal triangle.
When you allow the pedal point to be the centroid, the intersection of the medians of triangle ABC, where will the pedal triangle be located? Let's see ....
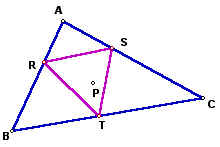
The pedal triangle will never lie outside of triangle ABC when the pedal point is the centroid of a triangle.
Let the orthocenter, the intersection of the altitudes of triangle ABC, be the pedal point.
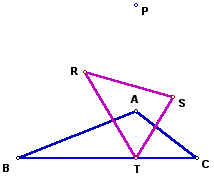
It happens to be that when the orthocenter becomes one of the vertices of the original triangle, two of the vertices of the pedal triangle collide into the orthocenter, giving a degenerate triangle or segment as the pedal triangle. To investigate this situation with Geometer's Sketch Pad, please click here.
Animations
What type of objects do you think will be formed when we trace the midpoints of the legs of the pedal triangle as the pedal point, P, follows the point of the circumcircle of triangle ABC? Click here for a Geometer's Sketch Pad animation demonstrating this.
What if we trace the midpoints of the legs of the pedal triangle again, however P follow the path of the circle centered at the circumcenter but a radius larger that of the circumcircle? Can you predict the types of figures that are being traced? Click here to see the results.