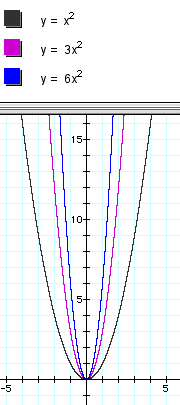
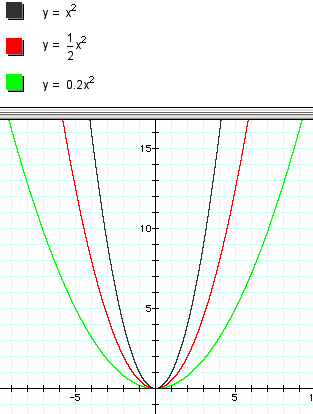
Observation 1:
|
|
|
Did you notice that for
values of the coefficient that were greater than 1, the graph
seemed to get thinner and for values between 0 and 1, the graph
seemed to get fatter. This gives us some idea of the shape of
the graph. However, what is really happening here is the graph
is stretching vertically for values of the coefficient greater
than 1 and it is compressing vertically for values of the coefficient
between 0 and 1. This is easier to understand if we look at the
data comparing one of these graphs to the parent function. The
chart below should be a comfortable example of this transformation
using the parent function and the data for the rule 
.
| x | f(x)=x^2 | f(x)=3x^2 |
| -5 | 25 | 75 |
| -4 | 16 | 48 |
| -3 | 9 | 27 |
| -2 | 4 | 12 |
| -1 | 1 | 3 |
| 0 | 0 | 0 |
| 1 | 1 | 3 |
| 2 | 4 | 12 |
| 3 | 9 | 27 |
| 4 | 16 | 48 |
| 5 | 25 | 75 |
Notice that for each value
of x, the y value is three times as large for the function 
as it is for the parent function. Compare
the y values of the parent function with those of the function
. Do you find that the y values
are five times smaller in the latter function (or one fifth as
large) for every x value?
Did you find that each graph was reflected or flipped over the x-axis so that each graph now had a vertex that was the maximum point on the graph? In fact, as you will discover in the final investigation of this unit, the graph is actually reflected over its vertex.