

The spreadsheet can be used for many different things. In this assignment, I will explore how EXCEL can be used to graph any function y = f(x).
Let's look at a graph of y = x^2 + x + 1 for x=-15 to 15. In EXCEL the x-values can be entered into the first column of cells and the y-values in the second column. The function can then be graphed and would look as follows.
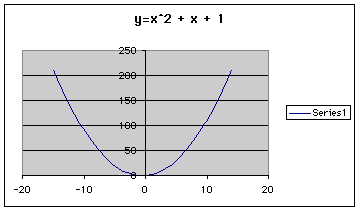
Other functions such as cosine and sine can be graphed as well. A graph of y = cos(0.5x) would look as follows.
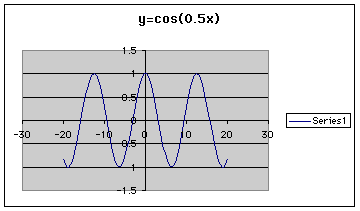
The spreadsheet can also be used to examine Fibonnaci sequence. The first column contains the Fibonnaci numbers using f(0)=1, f(1)=1, f(n)=f(n-1)+f(n-2). The second column is the ratio of each adjacent pair of terms in the Fibonnaci sequence. The third column is the ratio of every second term, the fourth column is the ratio of every third term, and the fifth column is the ratio of every fourth term. What do you notice about these ratios? Can you predict what would happen if you took the ratio of every fifth term?
| 1 | ||||
| 1 | 1 | |||
| 2 | 0.5 | 0.5 | ||
| 3 | 0.666666666666667 | 0.333333333333333 | 0.333333333333333 | |
| 5 | 0.6 | 0.4 | 0.2 | 0.2 |
| 8 | 0.625 | 0.375 | 0.25 | 0.125 |
| 13 | 0.615384615384615 | 0.384615384615385 | 0.230769230769231 | 0.153846153846154 |
| 21 | 0.619047619047619 | 0.380952380952381 | 0.238095238095238 | 0.142857142857143 |
| 34 | 0.617647058823529 | 0.382352941176471 | 0.235294117647059 | 0.147058823529412 |
| 55 | 0.618181818181818 | 0.381818181818182 | 0.236363636363636 | 0.145454545454545 |
| 89 | 0.617977528089888 | 0.382022471910112 | 0.235955056179775 | 0.146067415730337 |
| 144 | 0.618055555555556 | 0.381944444444444 | 0.236111111111111 | 0.145833333333333 |
| 233 | 0.618025751072961 | 0.381974248927039 | 0.236051502145923 | 0.145922746781116 |
| 377 | 0.618037135278515 | 0.381962864721485 | 0.236074270557029 | 0.145888594164456 |
| 610 | 0.618032786885246 | 0.381967213114754 | 0.236065573770492 | 0.145901639344262 |
| 987 | 0.618034447821682 | 0.381965552178318 | 0.236068895643364 | 0.145896656534954 |
| 1597 | 0.618033813400125 | 0.381966186599875 | 0.23606762680025 | 0.145898559799624 |
| 2584 | 0.618034055727554 | 0.381965944272446 | 0.236068111455108 | 0.145897832817337 |
| 4181 | 0.618033963166707 | 0.381966036833293 | 0.236067926333413 | 0.14589811049988 |
| 6765 | 0.618033998521803 | 0.381966001478197 | 0.236067997043607 | 0.14589800443459 |
| 10946 | 0.618033985017358 | 0.381966014982642 | 0.236067970034716 | 0.145898044947926 |
| 17711 | 0.618033990175597 | 0.381966009824403 | 0.236067980351194 | 0.145898029473209 |
| 28657 | 0.618033988205325 | 0.381966011794675 | 0.23606797641065 | 0.145898035384025 |
| 46368 | 0.618033988957902 | 0.381966011042098 | 0.236067977915804 | 0.145898033126294 |
| 75025 | 0.618033988670443 | 0.381966011329557 | 0.236067977340886 | 0.14589803398867 |
| 121393 | 0.618033988780243 | 0.381966011219757 | 0.236067977560485 | 0.145898033659272 |
| 196418 | 0.618033988738303 | 0.381966011261697 | 0.236067977476606 | 0.145898033785091 |
| 317811 | 0.618033988754323 | 0.381966011245677 | 0.236067977508645 | 0.145898033737032 |
| 514229 | 0.618033988748204 | 0.381966011251796 | 0.236067977496407 | 0.145898033755389 |
| 832040 | 0.618033988750541 | 0.381966011249459 | 0.236067977501082 | 0.145898033748377 |
You can do other sequences where f(0) and f(1) are arbitrary integers. Let's look at the sequence where f(0) = 5 and f(1) = 13. Each successsive term is found in the same manner as above f(n) = f(n-1) + f(n-2). In the chart below, the first column is the sequence, the second column is the ratio of to adjacent terms, and the third column is the ratio of every second term. What do you notice about this chart compared to the Fibonnaci sequence? Each ratio has the same limit. Do you think this is true for all such sequences?
| 5 | ||
| 13 | 0.384615384615385 | |
| 18 | 0.722222222222222 | 0.277777777777778 |
| 31 | 0.580645161290323 | 0.419354838709677 |
| 49 | 0.63265306122449 | 0.36734693877551 |
| 80 | 0.6125 | 0.3875 |
| 129 | 0.62015503875969 | 0.37984496124031 |
| 209 | 0.617224880382775 | 0.382775119617225 |
| 338 | 0.618343195266272 | 0.381656804733728 |
| 547 | 0.617915904936015 | 0.382084095063985 |
| 885 | 0.618079096045198 | 0.381920903954802 |
| 1432 | 0.618016759776536 | 0.381983240223464 |
| 2317 | 0.618040569702201 | 0.381959430297799 |
| 3749 | 0.618031475060016 | 0.381968524939984 |
| 6066 | 0.618034948895483 | 0.381965051104517 |
| 9815 | 0.618033622007132 | 0.381966377992868 |
| 15881 | 0.618034128833197 | 0.381965871166803 |
| 25696 | 0.618033935242839 | 0.381966064757161 |
| 41577 | 0.618034009187772 | 0.381965990812228 |
| 67273 | 0.618033980943321 | 0.381966019056679 |