This exploration attempts to address the following three questions:
A definition: The orthocenter of a triangle is the common intersection of the three lines containing the altitudes of a triangle.
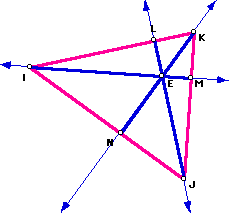
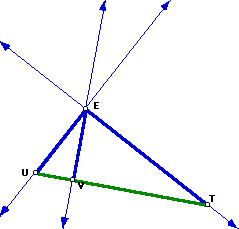
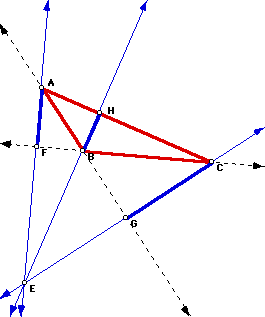
Here are some pictures of different types of triangles and their orthocenters, E.
 |
 |
 |
Notice that the orthocenter does not always lie inside the triangle. This fact should not be a surprise, since we know that the altitudes of a right triangle can coincide with the sides of the triangle and obtuse triangles have some altitudes that lie outside the triangle. In triangle ABC above, two of the altitudes, AF and CB, lie outside the triangle (except for an endpoint, points A and C.) Noticing this fact now is important for later, when we consider how the Nine-Point Circle behaves for different types of triangles.
Of course, the definition of orthocenter begs a question...how do we know the three lines containing the altitudes always intersect at one point? Click here for one way to prove that the lines containing the altitudes of a triangle are concurrent.
A definition: The Nine-Point Circle for any triangle passes through the three midpoints of the sides of the triangle, the three feet of the altitudes, and the three midpoints of the segments from the vertices of the triangle to the orthocenter. Note that this definition is NOT the only definition, and it is perhaps not the most elegant. For an alternative definition, see the investigations below.
Here's a picture of a Nine-Point Circle in an acute, scalene triangle:
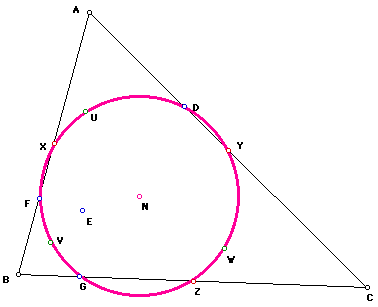
How to construct the Nine-Point Circle: Obviously, first you need to construct a triangle. ADVICE: Start your construction using lines for the sides of the triangle, not segments. (That is, draw line AB, line AC, line BC. You can then draw segments and hide the lines. If you follow this advice, later on points won't disappear from your Nine-Point Circle.
Then, with a little knowledge of The Geometer's Sketchpad, constructing midpoints of the sides (X, Y, and Z above), and the altitudes of the triangle (with feet D, F, and G above) is not terribly difficult. Even the construction of the midpoints of the segments AE, BE, and CE is not hard (points U, V, and W above.)
But, once you have the nine points, how do you create the circle? Of course, you need to find the circle's center (N above.) And this point N must be equidistant from all of those nine points...so, you might consider the locus of points equidistant from the endpoints of a segment...Click here for one way to find N. Once you locate N, of course, you can draw the circle by selecting the center and a point on the circle.
Download this GSP file of a Nine-Point Circle and drag the vertices of the triangle to explore these questions:
Happy Exploring...for this author's results, click here.
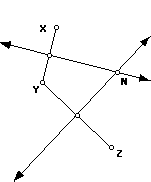
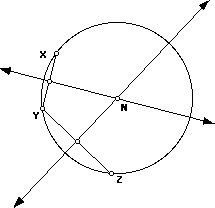
Finding the center of a circle given three (or more) points on a circle--
Draw two chords and find the perpendicular bisectors of each chord. All points on a perpendicular bisector of a segment are equidistant from the endpoints of that segment. So, the point where the perpendicular bisectors meet will be equidistant from all three points and will be the center of the circle passing through all three points.
 |
 |
 |
Back to Where I Was...