Investigation by Jake Klerlein

In this investigation I will present a proof that the medians of a triangle are concurrent. Also, the distance from the foot of the median to this point of concurrency is one third the length of the entire median.

Having said this, I must next mention the wisdom a mathematics professor shared one day. He stated that one should never try to prove three lines are concurrent, but rather one should prove some fact that means the concurrency exists.

Given triangle RTS with the midpoints M, J, and K to segments RT, RS, and TS respectively. First construct the line MJ. This construction creates a new triangle, RMJ.

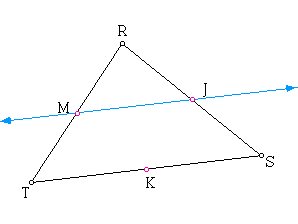
Considering the relationships between triangle RTS and triangle RMJ, we see that the two triangles share the angle at vertex R. Also, due to the fact that M is the midpoint of RT and J is the midpoint of RS, we know that . Thus by the SAS similarity theorem for triangles, we see that triangle RMJ is similar to triangle RTS. Since angle RMJ and angle RTS are corresponding angles of similar triangles we know that they must have congruent measures. This fact leads us to be able to say that line MJ is parallel to segment TS because angle RMJ and angle RTS are corresponding angles with respect to line MJ and segment TS. Also, knowing that triangle RMJ is similar to triangle RTS alerts us to the fact that . (Remember this fact for a necessary step in a few moments.)

 

Now construct the medians TJ and SM. Label their point of intersection C. See the diagram that follows for an illustration.

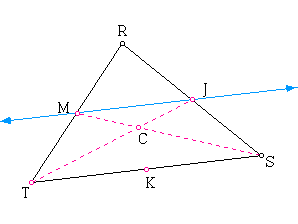
Here we see that angle JMC is congruent to angle CST and angle MJC is congruent to angle CTS because they are alternate interior angles in relation to transversals MS and JT respectively, which intersect the parallel lines MJ and TS. Therefore by the AA similarity theorem for triangles it can be shown that triangle MJC is similar to triangle STC. Recalling that we use the fact that triangle MJC is similar to triangle STC to understand that . Since the segments MC and CS comprise the median MS, we conclude that MC is one third the length of MS.

 

In order to show that the third median RK is concurrent to MS and TJ, draw the line MK and following the same process as above we can see that triangle TMK is similar to triangle TRS.

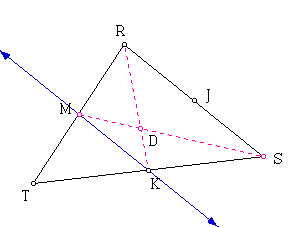
Both triangles contain the angle at vertex T, and , so by the SAS similarity theorem triangle TMK is similar to triangle TRS. Again we make note that since angle TKM and angle TSR are corresponding angles of similar triangles that they must be congruent and therefore line MK is parallel to segment RS. Also, we must recognize that . Now we construct the medians RK and MS. Label the intersection of these segments D.

As a note to the reader, I describe here what I wish to prove and why that means the medians are concurrent and divide each other as described at the onset of this investigation. If we show that RK intersects MS at D in such a fashion that , then the three medians are concurrent, C = D. We know this since JT divided MS by the same ratio that RK divided MS the JT and RK intersect MS at the same point making it so that all three medians must by concurrent. Thus the reader should pay close attention for the reasoning that C must be the same point as D.
By constructing the two medians shown below we now have more triangles to consider. Let's look at triangle MKD and triangle SRD.

 

We see in these triangles that angle DMK is congruent to angle DSR and angle DKM is congruent to angle DRS because they are alternate interior angles when the parallels MK and RS are intersected by transversals MS and RK respectively. Thus by the AA similarity theorem for triangles, triangle MKD is similar to triangle SRD. Since the corresponding sides must have lengths in the same ratio. Thus . Since MD and DS comprise the median MS, this statement of equal ratios tells us that MD is one third the length of MS. Since MC was also one third the length of the median, C must equal D. This fact means that all medians are concurrent. To conclude that each median is three times the length as the segment from the midpoint to the point of concurrency of the medians, we simply note that the point C (or D whichever the case may be as C = D) is on each median. From C to the foot of the median is half the distance from C to the vertex of the triangle, therefore the entire median is three times as long as the distance from C to the foot of the median.

Return to Jake's 6680 page