The graph of 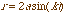 with a = 1 and k = 1. Notice this defines a radius 1 circle
centered at (1,pi/2).
with a = 1 and k = 1. Notice this defines a radius 1 circle
centered at (1,pi/2). |
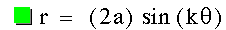 |
|
The graph of 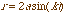 with a = 1 and k = 2. This is a 4 petal flower centered at
the origin with petals that appear to be 2 in length along their line of
symmetry.
with a = 1 and k = 2. This is a 4 petal flower centered at
the origin with petals that appear to be 2 in length along their line of
symmetry. |
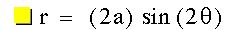 |
|
The graph of 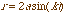 with a = 1 and k = +/- 3. This is a 3 petal flower centered
at the origin with petals that appear to be 2 in length along their line
of symmetry. Notice the negative inverts the original flower.
with a = 1 and k = +/- 3. This is a 3 petal flower centered
at the origin with petals that appear to be 2 in length along their line
of symmetry. Notice the negative inverts the original flower. |
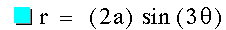
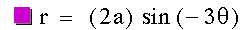
|
|
| Continuing to change the values for k will just continue
to add petals to the flowers observed. When k is an even number,
there are always 2k as many petals. The first petal counterclockwise
from the positive x-axis is at (2pi / 4k) radians and the
next petals are (2pi / 2k) radians counterclockwise from there. When
k is an odd number, there are k petals. One petal will be
on the negative y axis, with the rest (2pi / k) radians counterclockwise
from there. A negative value for k only has an observable effect
on odd values of k, as seen in the final example above. This flips
the image of the graph with positive k over the horizontal axis.
|
Next to look at the graphs of the form  .
First consider when a = 1 and k = 1. Notice this defines a
radius 1 circle centered at (1, 0). As you may expect, there is a clockwise
rotations of pi/2 compared with the same function that replaces the cosine
with sine (see the green circle above). .
First consider when a = 1 and k = 1. Notice this defines a
radius 1 circle centered at (1, 0). As you may expect, there is a clockwise
rotations of pi/2 compared with the same function that replaces the cosine
with sine (see the green circle above). |
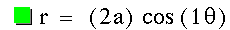 |
|
The graph of  with a = 1 and k = 2. This is a 4 petal flower centered at
the origin with petals that appear to be 2 in length along their line of
symmetry. Again, there is a clockwise rotations of pi/2 compared with the
same function that replaces the cosine with sine (see the yellow flower
above).
with a = 1 and k = 2. This is a 4 petal flower centered at
the origin with petals that appear to be 2 in length along their line of
symmetry. Again, there is a clockwise rotations of pi/2 compared with the
same function that replaces the cosine with sine (see the yellow flower
above). |
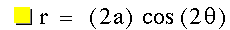 |
|
The graph of  with a = 1 and k = +/- 3. This is a 3 petal flower centered
at the origin with petals that appear to be 2 in length along their line
of symmetry. Again, there is a clockwise rotations of pi/2 compared with
the same function that replaces the cosine with sine. However, notice that
both graphs do not appear. In fact, both are present and the same inversion
about the x-axis occurs as seen in the sine function above. However,
because of the pi/2 rotation, this inversion maps the flower right back
to itself.
with a = 1 and k = +/- 3. This is a 3 petal flower centered
at the origin with petals that appear to be 2 in length along their line
of symmetry. Again, there is a clockwise rotations of pi/2 compared with
the same function that replaces the cosine with sine. However, notice that
both graphs do not appear. In fact, both are present and the same inversion
about the x-axis occurs as seen in the sine function above. However,
because of the pi/2 rotation, this inversion maps the flower right back
to itself. |
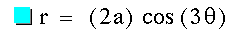
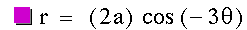
|
|
| Continuing to change the values for k will just continue
to add petals to the flowers. This behavior observed in the cosine functions
summarily acts the same as the sine examples above. When k is an
even number, there are always 2k as many petals. The first petal
counterclockwise from the positive x-axis is at 0 radians of counterclockwise
rotation and the next petals are (2pi / 2k) radians counterclockwise
from there. When k is an odd number, there are k petals. One
petal will be on the positive x axis, with the rest (2pi / k)
radians counterclockwise from there. A negative value for k only
has no observable effect on values of k, as seen in the final example
above. |

