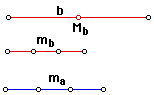
---

One side b and two medians to sides a and b

---

By: Tim Lehman

---

Given:

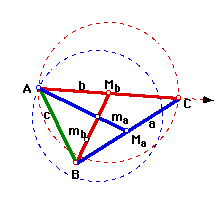
Construction:

First, construct the median to side b. We know vertices A and C are on the circle centered at the midpoint of side b with a radius of a half of length b. Because the centroid cuts the medians in a 2 to 1 ratio, the vertex A is on the circle centered at the centroid with a radius of 2/3 the length of the median to side a. The vertex A is at the intersection of these two circles. Vertex C can be found because it is on the line through vertex A and the midpoint of side b and on the first circle drawn.

Click here for a GSP sketch of the above construction.