Final Project

Kim Seay

EMAT 6680

Fall 2000

PART A:

This problem asks us to first consider any triangle ABC. Then, select any any point "P" inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Now, explore the relationship of (AF)(BD)(EC) and (FB)(DC)(EA). I have create one example of this below:

Click here to open a file of this figure. You can click on any point and drag the triangle around. You can see that the two products are still equal. If the two products are always equal, then the ratio of the products will always be 1.

PART B:

Conjecture: The ratio of of (AF)(BD)(CE)=(BF)(CD)(AE)

Given: Lines l, m, and p are parallel to each other.

Proof

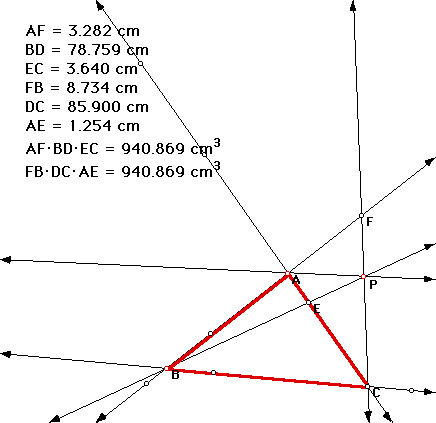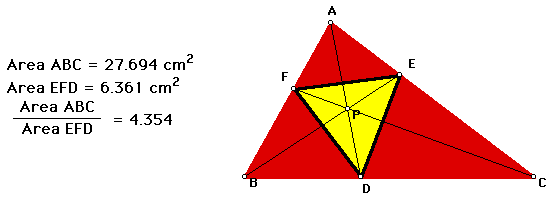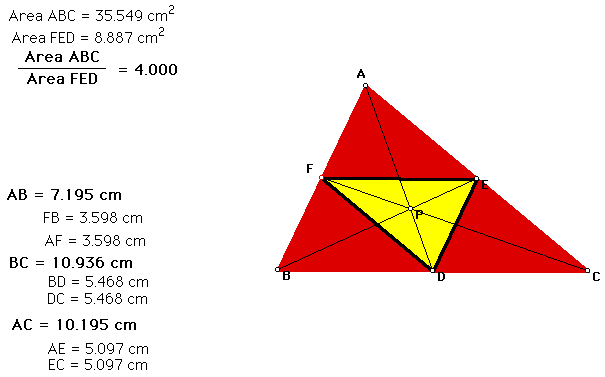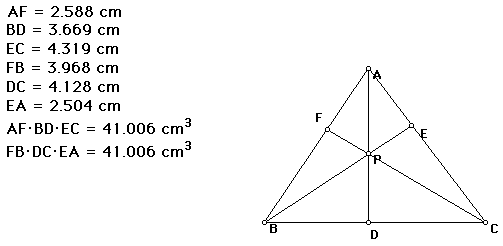
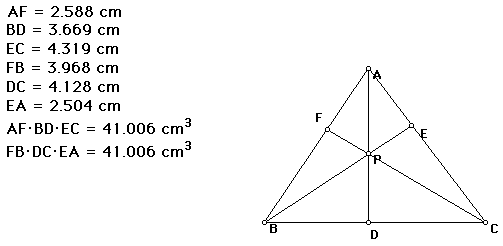
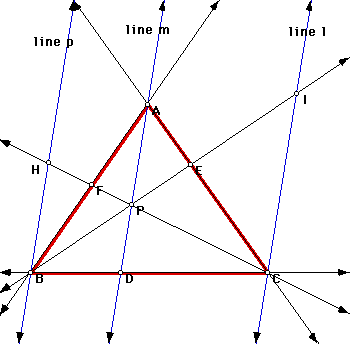
1. <AEP is congruent to <IEC -Vertical <s are congruent

2. <APE is congruent to <CIE - When two parallel lines are cut by a transversal, alternate interior ,s are congruent.

3. Triangle APE is similar to triangle CIE - Angle Angle similarity postulate

4. EA/EC=AP/CI - Corresponding sides of similar triangles are proportionate

5. <BFH is congruent to <AFP - Vertical <s are congruent

6. <FHB is congruent to <FPA -When two parallel lines are cut by a transversal, alternate interior ,s are congruent.

7. Triangle BFH is similar to triangle AFP- Angle Angle similarity postulate

8. BF/AF=BH/AP- Corresponding sides of similar triangles are proportionate

9. <BPD is congruent to <BIC - When two parallel lines are cut by a transversal, Corresponding angles are congruent.

10. <PBD is congruent to <IBC - Reflexive property

11. Triangle BDP is similar to triangle BCI- Angle Angle similarity postulate

12. DB/CB=PD/CI- Corresponding sides of similar triangles are proportionate

13. <PCD is congruent to <HCB - Reflexive property

14. <CPD is congruent to <CHB - When two parallel lines are cut by a transversal, Corresponding angles are congruent.

15. Triangle PCD is similar to triangle HCB- Angle Angle similarity postulate

16. PD/HB=CD/BC -Corresponding sides of similar triangles are proportionate

17. (PD)(BC)=(HB)(CD) - Cross multiplication from line 16

18. (DB)(CI)=(BC)(PD) - Cross multiplication from line 12

19. BH=((AP)(BF))/(AF) - Multiplication and division from line 8

20. CI = ((AP)(EC))/(AE) - Multiplication and division from line 4

21. (PD)(BC)= ((AP)(BF)(CD)) / (AF) - Substitution lines 17 and 19

22. ((DB)(AP)(EC)) / (AE) = (PD)(BC) substitution lines 18 and 20

23. ((AP)(BF)(CD)) / (AF) = ((DB)(AP)(EC)) / (AE) Reflexive-lns 21 & 22

24. (AE)(AP)(BF)(CD) = (AF)(DB)(AP)(EC) - Multiply both sides by (AF)(AE)

25. (AE)(BF)(CD)=(AF)(DB)(EC) -Divide both sides by (AP)

 

Consider the case where point p lies outside the triangle:

 

Click here to open an example of this and drag point p to varios locations outside of the triangle.

 

PART C:

When point p is inside the triangle, we can use segments to create a second triangle EFD. The ratio of the areas of triangle ABC to Triangle EDF will always be greater than or equal to 4. I have shown one example of this below.

Click here to drag point p around inside the triangle and watch the observe what happens to the ratio of areas between the two triangles.

The rare case where the ratio is equal to four occurs when the points F, D, and E arethe midpoints of their respective sides on triangle ABC. In other words, point p is the centroid of triangle ABC.

 

 

RETURN