Almost a Square
Kim Seay
EMAT 6680
I begin this exploration
with any square that has sides of integral length. I will start
with the simple case of a square with a side length equal to 2cm.
 The next step is to find
the rectangle that has an area of one integer less than the original
square (n^2 - 1), and also has sides of integral length.
The next step is to find
the rectangle that has an area of one integer less than the original
square (n^2 - 1), and also has sides of integral length.

Finding a Pattern
The challenge, is to find
a pattern that can be applied to all such squares to find a rectangle
that has an area of one integer less than the square. I explored
a few more constructions before I was able to see the pattern.


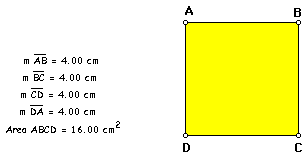

As I began to see the pattern
emerge, I made a table of squares with side lengths of 3cm - 20cm
to test my theory.
| n |
n-1 |
n+1 |
(n-1)*(n+1) |
n^2 |
| 3 |
2 |
4 |
8 |
9 |
| 4 |
3 |
5 |
15 |
16 |
| 5 |
4 |
6 |
24 |
25 |
| 6 |
5 |
7 |
35 |
36 |
| 7 |
6 |
8 |
48 |
49 |
| 8 |
7 |
9 |
63 |
64 |
| 9 |
8 |
10 |
80 |
81 |
| 10 |
9 |
11 |
99 |
100 |
| 11 |
10 |
12 |
120 |
121 |
| 12 |
11 |
13 |
143 |
144 |
| 13 |
12 |
14 |
168 |
169 |
| 14 |
13 |
15 |
195 |
196 |
| 15 |
14 |
16 |
224 |
225 |
| 16 |
15 |
17 |
255 |
256 |
| 17 |
16 |
18 |
288 |
289 |
| 18 |
17 |
19 |
323 |
324 |
| 19 |
18 |
20 |
360 |
361 |
| 20 |
19 |
21 |
399 |
400 |
Now the pattern is clear
to see. To find the rectangle with an area equal to one integer
less than any square (with integral sides) simply use the sides
n-1 and n+1. This will always work, because (n-1)(n+1) = n^2 +n
-n - 1 = n^2-1.
Conclusion:
I like this exploration,
because I have never thought about the difference of squares formula
from this perspective. I memorized it over a decade ago, but never
really pondered what it meant. This exploration made me do this,
and I think it would do the same for students.
Return






