
Department of Mathematics Education
J. Wilson, Emat 6680

Lesson # 6
By Jan White
Construct a triangle and its medians. Construct a second
triangle with the three sides having the lengths of the three medians from
your first triangle. Find some relationship between the two triangles.
(E.g., are they congruent? similar? have same area? same perimeter? ratio
of areas? ratio or perimeters?) Prove whatever you find.
I will show that the areas of the triangle ABC and the medial triangle EFG are 4:1 and that the perimeters of the triangles are in the ratio of 2:1.
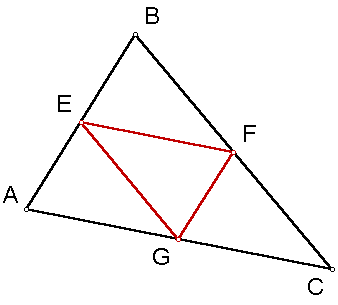
AB/AE as CB/CF, therefor EF is parallel to AG.
AC/AG as BC/CF, therefor AE is parallel to FG.
Two sets of parallel segments intersect to form a parallelogram. The segment EG will divide the parallelogram into two similar and equal in area triangles AEG and EFG.
The same can be said for parallelograms EBFG and EGCF. Each of the triangles will have the same areas.
Since the triangle is divided into 4 triangles of equal areas, then the ratio of triangle ABC to the medial triangle EFG is 4:1
The perimeter of triangle ABC and triangle EFG are in the ratio of 2:1.
It was previously shown that triangle ABC is similar to triangle EFG. Since AB/AE and E is the midpoint of AB then AB/AE = AB/FG = 2/1. Similarly AC/AG = AC/EF = 2/1 and BC/BF = BC/EG = 2/1. Since all the segments for each triangle are in a 2:1 ratio then their perimeters are also in a 2:1 ratio.
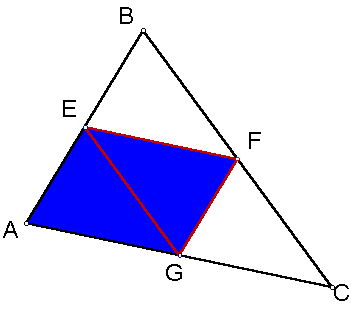
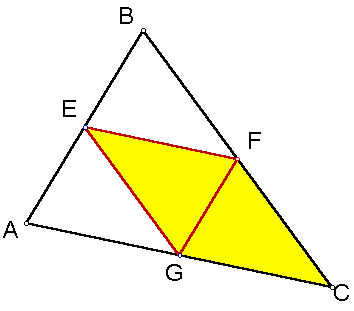
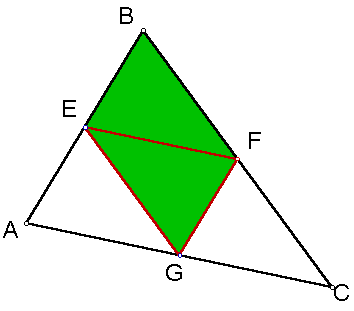
For a more dynamic look, click here and try dragging one of the vertices of the large triangle. You will see that the areas are in a 4:1 ratio and the perimeters are in a 2:1 ratio.