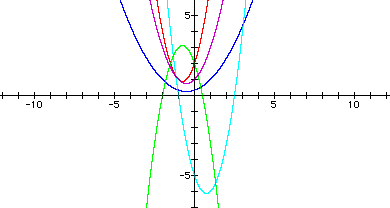
At the start of the exploration, the y= ax^2 +bx+c form of the quadratic equation is graphed with random rational numbers as a, b, and c. The values of a, b, and c are varied between positive and negative numbers, numbers less than and greater than 1.

i) Starting specifically with the graph where a=2, b=3, and c=-4, the graph becomes as follows.....
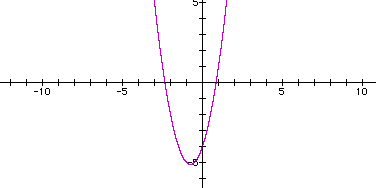
By modifying the x-variable to an x-4, the graph shifts 4 coordinates to the right---in the positive x direction.
y= 2(x-4)^2 +3(x-4) -4
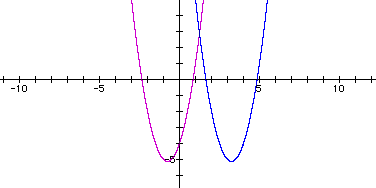
From this it can be deduced that changing x to x+4 would shift the graph/vertex 4 coordinates in the negative x direction. See the graph here.
ii) Since modifying the x-variable will shift the vertex of the parabola along the x-axis, apparently modifying the y-variable would shift the parabola in a vertical direction. Consider y-7 = 2(x+4)^2 +3(x+4) -4. Subtracting seven from y moves the graph in the positive y-direction--up. The vertex is then in the quadrant 2. In the graph the parabola appears only in the second quadrant, but eventually the right side of the parabola (by right side, I mean graph to the right of the axis of symmetry--x equals approximately -4.8) would cross over the y-axis into the first quadrant. Simplifying the expression from above yeilds
![]()
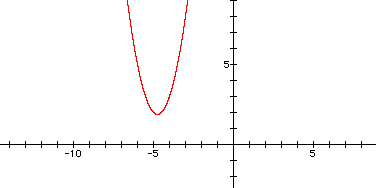
It is not possible to have a parabola completely in one quadrant since all parabolas gradually widen towards infinity....for this particular equation, the parabola widens towards y= positive infinity. Click here for a zoomed out image.
iii) What if we want a parabola that faces downward....a parabola with the same vertex, but gradually widening in the y = negative infinity direction? Knowing a negative had to affect the graph in some way, I first altered the expression to negative y equals. The following graph appeared, but the vertex was not the same.
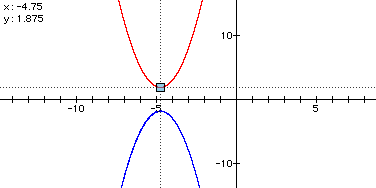
The vertex is shown on the concave up parabola to be the minimum x= -4.75, y= 1.875. (This is the exact minimum...I double checked the accuracy using calculus and derivatives.) Conversely, the maximum of the concave down parabola is at y = -1.875. Before, the parabola was shifted vertically upwards by subtracting a constant from the y-variable. The difference between the two vertices is 1.875-1.875 =3.75, so it is subtracted to move it upwards. Be careful when doing this because adding it to y would give you this.
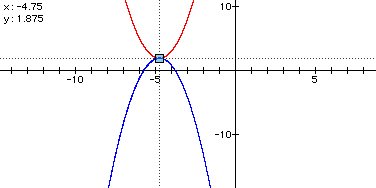
Although is hard to tell in the graph, the trace is actually on the vertex of the blue parabola, and notice is has the same vertex as the red one above it. To see the image without the concave up parabola, click here.