As c changes...
In all previous examples, the value
of c has been 0. How does changing the value of c affect the sine
curve? Once again, let's explore with several examples:
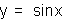
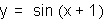
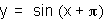
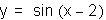
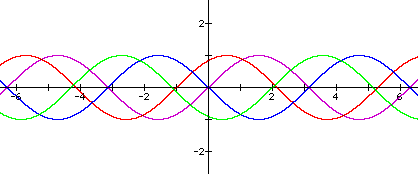
When c=0, the graph of y=sin x passes through
..., x=-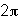 , x=-
, x=-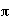 , the
origin, x=
, the
origin, x=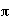 , x=
, x=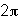 ,....
For the graph of y=sin(x+1), c=1. This curve passes through the following
points: ..., x=-
,....
For the graph of y=sin(x+1), c=1. This curve passes through the following
points: ..., x=-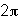 -1, x=-
-1, x=-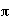 -1,
x=-1, x=
-1,
x=-1, x=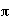 -1, x=
-1, x=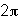 -1,....
The graph has been shifted or translated to the left by -1 units
along the x-axis.
-1,....
The graph has been shifted or translated to the left by -1 units
along the x-axis.
In general, the graph of y=sin (x+c)
translates to the left on the x-axis by c units, if c is positive.
Now, let's consider what happens when
c is negative. From our example y=sin(x-2), we can name the points where the curve crosses
the x-axis. These are: ..., x=-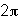 +2,
x=-
+2,
x=-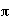 +2, x=2, x=
+2, x=2, x=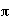 +2,
x=
+2,
x=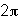 +2,.... So, the graph appears to
be shifted to the right along the x-axis by 2 units.
+2,.... So, the graph appears to
be shifted to the right along the x-axis by 2 units.
In general, if c is negative, the graph
of y=sin (x+c) translates to the right along the x-axis by a distance
of  units.
units.
