Polar Equations
Investigate the graphs of:
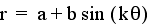
in comparison to the graphs
of:
Begin by exploring examples where a
= b = 1 and k is even. Below k = 0, 2, 4.
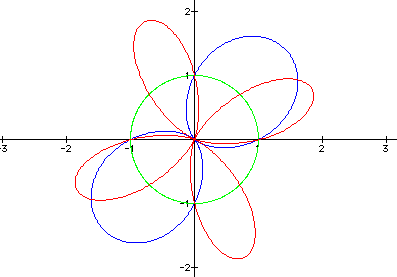
Notice that each graph is symmetric
with respect to both the x-axis and the y-axis.
Also, the lengths of each leaf are the
same as the cosine graphs, except when k = 0. Normally, the length
of each leaf is equal to 
. However, when
k = 0, the length of the radius of the circle is equal to 
.
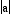Another difference lies in the orientation
of the graphs. Each sine graph can be obtained by rotating its
corresponding cosine graph by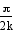 
radians.
Now examine the graphs when k is odd.
Below k = 1,
3, 5.
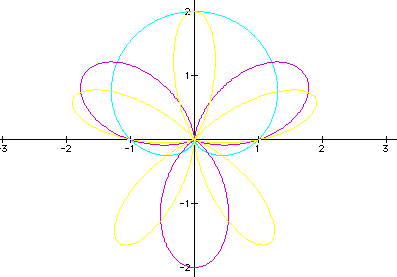
In this case, each graph is symmetric
with respect to the y-axis only. Thus, when negative values of
a and b are used (where a = b still), the graph will be reflected
across the x-axis. The symmetry is opposite of the cosine graphs.
The lengths of each leaf are the same
as the cosine graphs. Each leaf has a length of .
Again, each sine graph can be obtained
by rotating its corresponding cosine graph by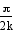
radians.
Change the values of a and b yourself
as you watch the graph
of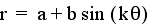 
change when k varies between -10
and 10.
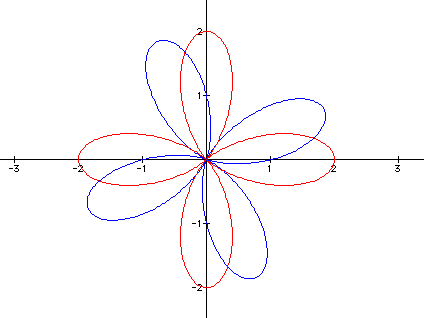
Here is an illustration of the differences
in orientation between the cosine and sine graphs. The graph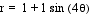 
is displayed in blue, while the graph of 
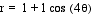is displayed in red.
The sine graph can be obtained from the cosine graph by a rotation
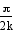of radians. View
an animation of this comparison as k
varies between -10 and 10.
Return to the
graphs of .