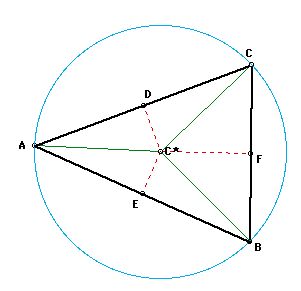
We wish to prove that segment AC* is congruent to segment BC*.  We will use this congruence later in the main proof.
 

• Since D is the midpoint of segment AC, we know that AD is congruent to DC.

• Also, since C*D is a perpendicular, we know that both angle C*DA and C*DC are right angles.  Right angles are always congruent, so angle C*DA is congruent to angle C*DC.

• C*D is congruent to itself by the identity property.

Hence, by the Side-Angle-Side (SAS) congruence criterion, Triangle ADC* is congruent to Triangle CDC*.  Since corresponding parts of congruent triangles are congruent, AC* is congruent to CC*.

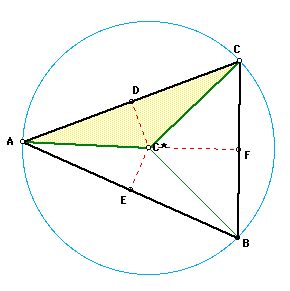
Similarly:

• Since F is the midpoint of segment BC, we know that BF is congruent to FC.

• Also, since C*F is a perpendicular, we know that both angle C*FB and C*FC are right angles.  Right angles are always congruent, so angle C*FB is congruent to angle C*FC.

• C*F is congruent to itself by the identity property.

Hence, by the Side-Angle-Side (SAS) congruence criterion, Triangle BFC* is congruent to Triangle CFC*.  Since corresponding parts of congruent triangles are congruent, BC* is congruent to CC*.

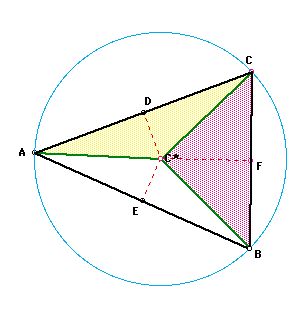
Since AC* is congruent to CC* and BC* is congruent to CC*, AC* is congruent to BC* by transitivity.  This makes sense since AC*, BC*, and CC* are all radii of the circumcircle.

Return to Summer's Main Page