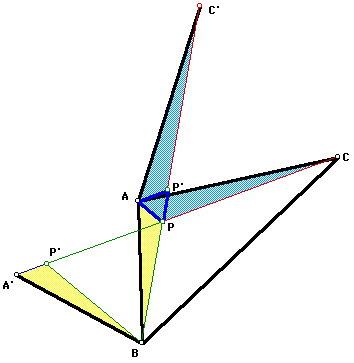Assignment #6
Fermat Point
by
Summer D. Brown
Problem: Consider any triangle ABC.
Find a construction for a point P such that the sum of the distances
from P to each of the three vertices is a minimum.
Construction:
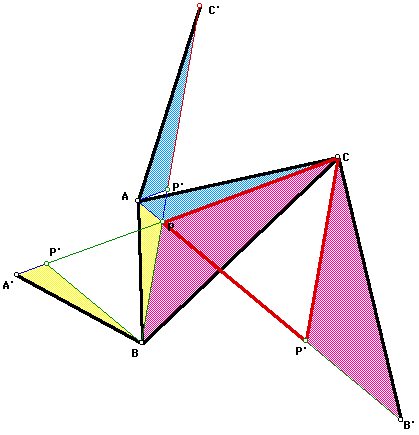
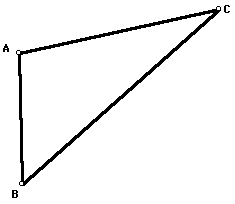
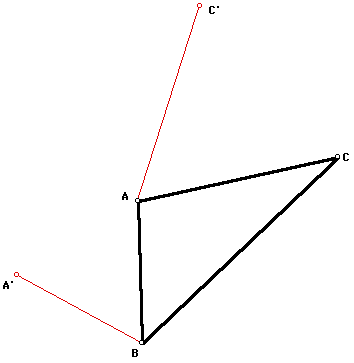
Start with any triangle ABC.
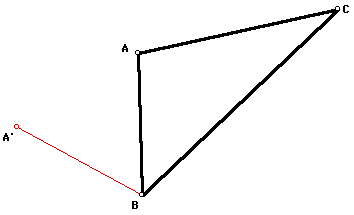
Mark one of the vertices as a center
of rotation. Rotate one of the adjacent sides of the triangle
60 degrees about the marked center.
Repeat a rotation by 60 degrees again
using another vertex as the center of rotation and one of its
adjacent sides.
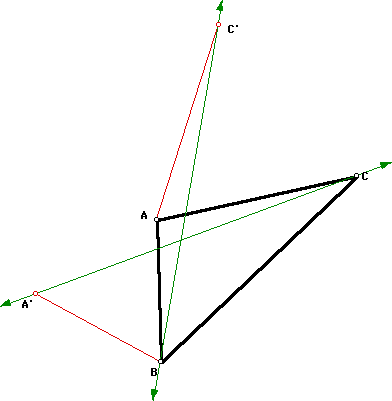
Next, construct a line through points
A' and C and another line through points C' and B.
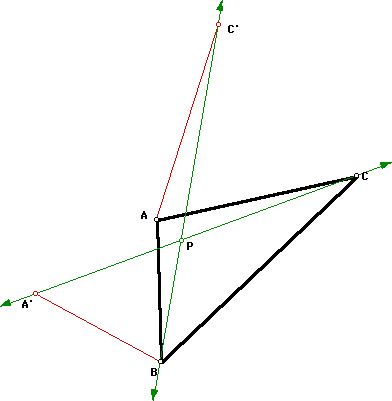
The intersection point P of these two
lines will be the point such that the sum of the distances from
P to each of the vertices is a minimum. This point P is called
the Fermat Point. Open a GSP
script for the construction of the Fermat point for any triangle.
So, the sum of the distances AP, BP, and CP will be the minimum
sum of distances from any point to each of the three vertices.
Proof:
Prove that P is the point such that
the sum of the distances from P to each of the three vertices
of triangle ABC is a minimum. Call such a point P the Fermat point
of triangle ABC.
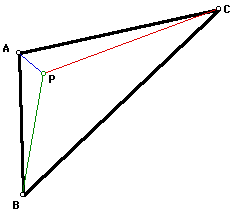
Take one of the triangles formed by
the vertices of triangle ABC and point P. First, I will use triangle
APB. Rotate triangle APB 60 degrees around vertex B.
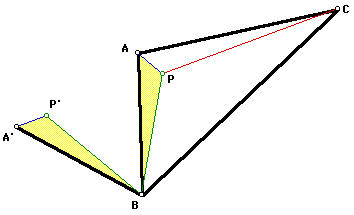
Distances are preserved under a rotation.
Thus, AP = A'P' and BP = BP'. The angle PBP' = 60 degrees since
we rotated the triangle by 60 degrees. Since a(PBP') = 60 degrees
and BP = BP', we can form the equilateral triangle PBP', which
is outlined in green below.
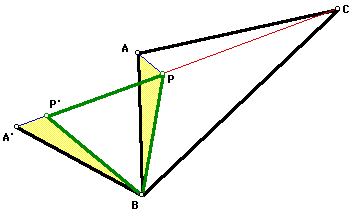
We have formed a straight line segment
A'C using the lengths of the segments AP, BP, and CP. We will have the minimum distance when the
segments form a straight line. Thus, the point that will create
this minimum distance must lie somwhere on this line.
Perform a similar rotation around vertex
A with triangle APC to find another straight line containing all
three segments. Equilateral triangle APP' is highlighted in blue.
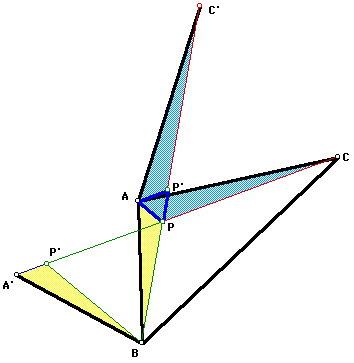
Once again, we have formed a straight
line segment BC' using the lengths of segments AP, BP, and CP. The Fermat point must lie somewhere on this
line as well. Thus, the Fermat point must lie at the intersection
of the lines A'C and BC'. Therefore, P is the point such that
the sum of the distances from P to each of the three vertices
of triangle ABC is a minimum.
Note that you can also use triangle
BPC to rotate around vertex C in a similar fashion as above. The
straight line segment AB' formed containing the lengths AP, BP, and CP will also pass
through the Fermat point P.