p » 355/113 = 3 + 16/113 = 3 +
42/(72 + 82) » 3.1415929
In this construction, we
will construct a segment having a length of
355/113 = 3 + 16/113 = 3 + 42/(72
+ 82) » 3.1415929,
which is a little less than p + 0.0000003.
Suppose
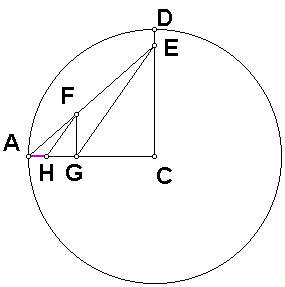
we are given a circle c1 with center C through the point A such that
AC = 1. Construct the radius DC
perpendicular to AC. We need to find
the point E so that EC is 7/8. To do
this, construct the midpoint M1 of segment CD. Construct the midpoint M2 of
segment M1D. Construct the
midpoint of segment M2D, and label it E. Construct segment AE.
Applying the Pythagorean Theorem to triangle ACE, we have
(AE)2 = (EC)2
+ (AC)2 = (7/8)2 + 12 = (72 + 82)/82.
Now
we need to find the point F on AE so that AF = ½. To do this, construct the midpoint M3 of segment
AC. Construct the circle c2
centered at A through the point M3.
Construct the intersection of circle c2 and segment AE, and
label it F. The length of segment AF is
½.
Construct
the line through F parallel to CD.
Construct the intersection of this line and the segment AC, and label it
G. Construct the segment FG. Angles AFG and AEC are congruent because
when two parallel lines (FG and EC) are cut by a transversal (AE),
corresponding angles are congruent.
Angles GAF and CAE are congruent because they are the same angle, so
triangles AFG and AEC are similar by angle-angle similarity. Therefore, FG/AF = EC/AE, so we have
FG = (AF)(EC)/(AE) = ½ *
(7/8) * Ö(82/(72
+ 82)) = (7/2) * Ö(72 + 82).
Construct
the segment EG, and construct the line through F parallel to EG. Construct the intersection of this line and
the segment AC, and label it H. When
two parallel lines (FH and EG) are cut by a transversal (AC), corresponding
angles are congruent, so angles FHA and EGA are congruent. Angles FAH and EAG are congruent because
they are the same angle, so triangles AFH and AEG are similar by angle-angle
similarity. Therefore, AH/AF = AG/AE,
so AH = (AF)*(AG)/AE. Similarly, angles
FGA and ECA are congruent, so triangles AFG and AEC are similar by angle-angle
similarity. Thus,
AG/FG = AC/EC = 1/(7/8) =
8/7.
So AG = (8/7)*(FG).
We now have
AH = (AF)*(8/7)*(FG)/AE =
(1/2)*(8/7)*(7/2)/Ö(72 + 82)
* 8/Ö(72 + 82) = 16/(72
+ 82) = 42 / (72 + 82).
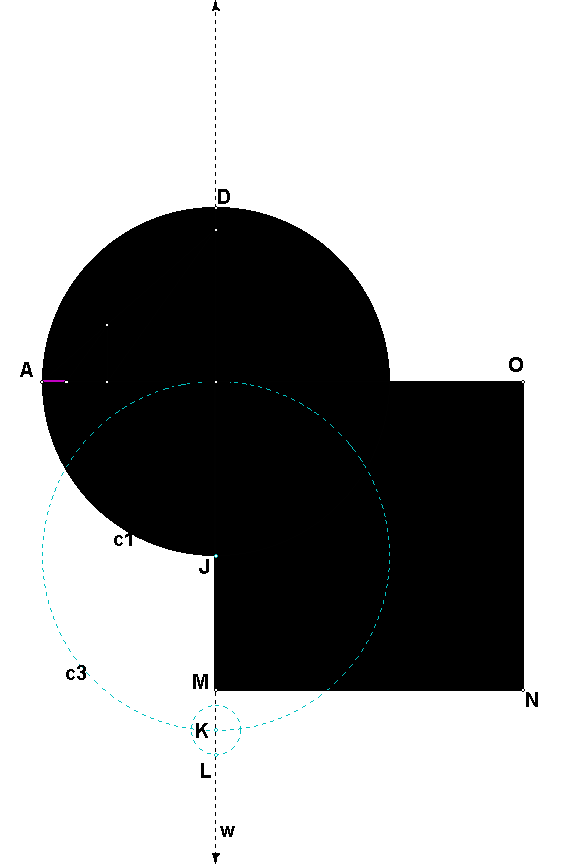
Since we can approximate p by 3 + 42/(72 + 82),
we need to construct a segment of length 3 + AH. First, construct the line w that passes through C and D. Construct the intersection of this line and
the circle c1, and label the point of intersection that is different
from D with the letter J. Construct the
circle c3 with center J though the point C. Construct the intersection of this circle
and the line w, and label the point that is different from C with the letter
K. Now the length of DK is 3. Construct the circle c4 with
center K and radius of length AH.
Construct the intersection of this circle and the line w, and label the
point that is on the opposite side of K from J with the letter L. Construct the segment DL. The length of DL is 3 + 42/(72
+ 82).
We want to construct a
square having an area of p, so each side needs to have
a length of Öp.
Since the length of DL is approximately equal to p, use the script to construct a segment of
length ÖDL. One endpoint of the segment is the point
C. Label the other one M. Now use the script for constructing a square
to construct the square CMNO. The area
of the square is approximately equal to the area of the original circle.
Click here for a GSP sketch of
the construction.