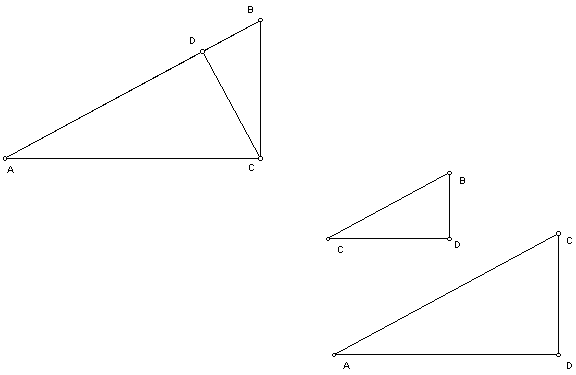
Proof for the Square Root Construction

Theorem: The altitude on the hypotenuse of a right triangle is the geometric mean of the segments of the hypotenuse. In other words, if ABC is a triangle with right angle at vertex C, and CD is the altitude from C to the side AB, then CD is the geometric mean of AD and DB.

Proof:

Let triangle ABD be a right triangle with altitude CD from C to the side AB. Then angles BDC and CDA are right angles. Since angle ACB is a right angle, angles CAB and CBA are complementary. Since angle CDA is a right angle, angles CAB and DCA are complementary. Since angles DCA and CBA are complementary to the same angle, they are congruent. Angle DBC is the same as angle CBA. So angles DCA and DBC are congruent. Since angles DCA and DBC are congruent and angles CDA and BDC are right angles, triangles CDA and BDC are similar by angle-angle similarity.

Since corresponding sides of similar triangles are proportional, AD/CD = CD/BD. Cross-multiplying yields (CD)² = (AD) × (BD), so CD is the geometric mean of AD and BD.