Investigation for the graph of
Problem: Let's
look at the graphs of
![]() ,
,
after fixing two of the values for a, b, and c.
Let's take a look at
![]()
for c = -3, -1, 0, 1, 3.
The graphs look like
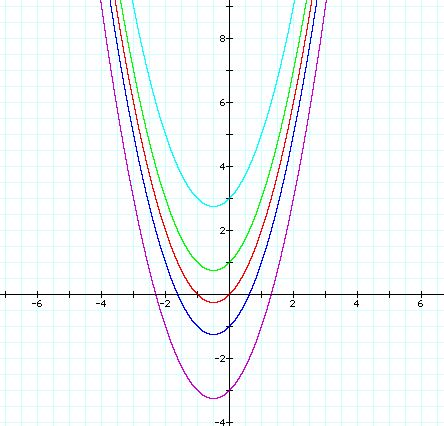
We can expect the graphs go up as c value increases and the graphs go down as c vaule decreases.
Let's take a look at
![]()
for b= -4, -2, 0, 2, 4.
The graphs look like
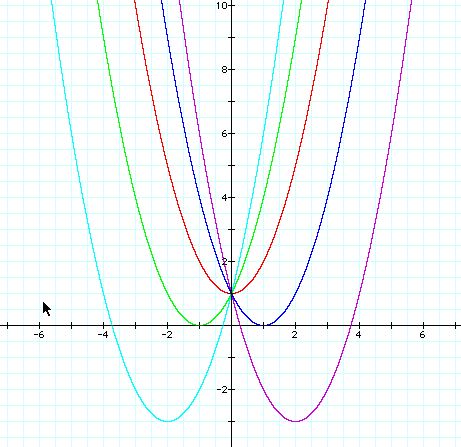
The parabola always passes through the same point on the y-axis ( the point ( 0, 1 ) with this equation ) For b < -2 the parabola will intersect the x-axis in two points with positive x values and vertex is positive For 0 < b < -2, the parabola will not intersect the x-axis and vertex is positive. For 0< b < 2, the parabola will not intersect the x-axis and vertex is negative. For b > 2, the parabola will intersect the x-axis in the two points with negative x values and vertex is negative.
Let's take a look at
![]()
for a = -3, -1, 0, 1, 3.
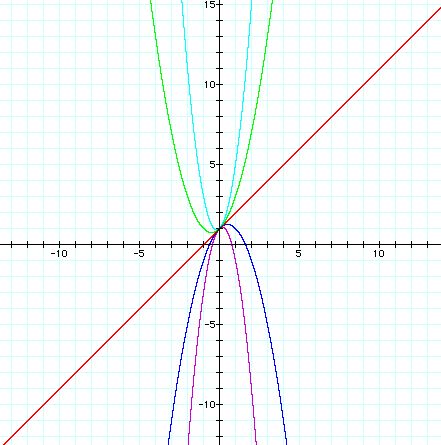
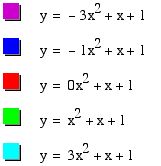
The parabola always passes through the same point on the y-axis ( the
point ( 0, 1 ) with this equation ). If a = 0, then the parabola becomes
the line eqation in the plane. For a < 0, the graphs are concave down.
For a > 0, the graphs are concave up.
In the parabola, a value decedes concave up or down, b value decides
whether the vertex is on the positive or negative and c value decides whether
the graphs go down or up in the same shape.
Return to the Top