Pedal point and Pedal triangles

First, I will create a script for the general construction of a pedal triangle to triangle ABC where P is any point in
         the plane of ABC.
If you want to check the script, please click here.

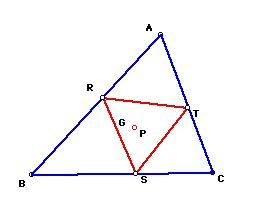
If pedal point P is the centroid(G) of triangle ABC, then the pedal triangle looks like

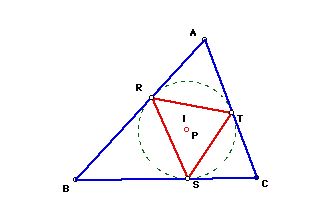
If pedal point P is the incenter( I ) of triangle ABC, then the pedal triangle looks like

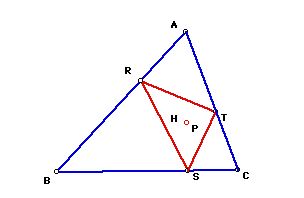
If pedal point P is the orthocenter(H) of triangle ABC, then the pedal triangle looks like

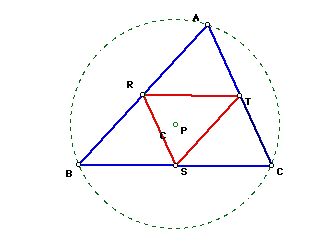
If pedal point P is the circumcenter(C) of triangle ABC, then the pedal triangle looks like

If you want to check GSP, click here.

If pedal point P is on a side of the triangle, then pedal point P equals to R , S, and T and
the pedal triangles look like

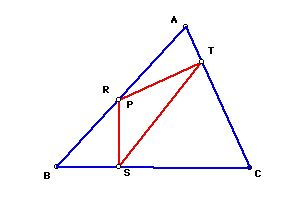
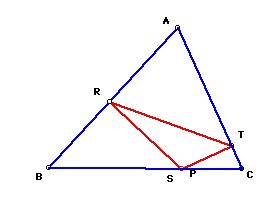
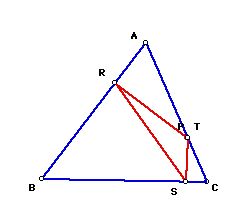
If pedal point P is one of the vertices of triangles ABC, the pedal triangle looks like

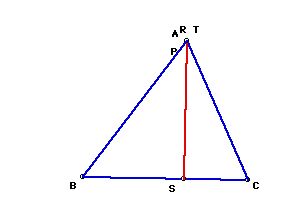
When pedal point p is A, the points of A, R, T , and P are the same.
So, the pedal triangle become a line.
Similarly, if pedal point p is B or C, then the pedal triangle become the line passing through B or C respectively.

Simson Line

All conditions in which the three vertices of the Pedal triangles are colinear are that pedal point P is on the cicumcircle of the triangle ABC.

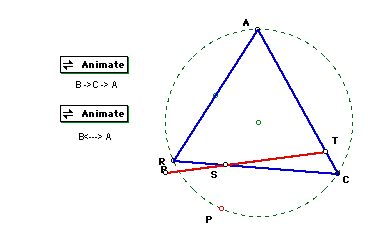
If you want to check this fact by GSP, please click here