The Pedal Triangle is formed by using a given triangle and any point in the plane P.  The Pedal Triangle is formed by constructing the perpendiculars to the sides (extended if necessary) of the given triangle from the Pedal Point P. In this assignment, we are going to explore the different locations of the Pedal Triangle when the location of the Pedal Point P has been varied.

   To look at a GSP script of the formation of the Pedal Triangle given the three points on the original triangle and the Pedal Point P, click here.

Pedal Triangle GSP

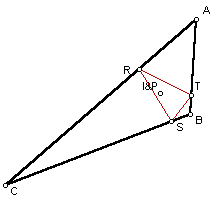
   In our first example, P is any point outside of triangle ABC.  Our Pedal Triangle is triangle RST for each example.  Our given point is P for each example.

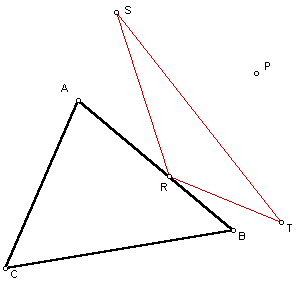
    In this example, the Pedal Triangle is completely outside of the given triangle ABC.  Next lets look at a point P that is close to the original triangle.

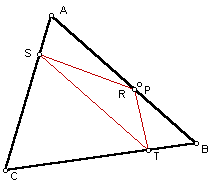
    In this sketch, the Pedal Triangle is completely inside of the original triangle ABC.  Next lets look at a case where the Pedal Point is inside of the given triangle.

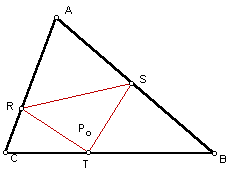
    In this sketch, the Pedal Triangle is also inside of the given triangle.  Therefore, we have seen from these example that the placement of the Pedal Point P does effect where the Pedal Triangle is located.  In the next set of examples, we will look at specified placements of P and how that effects the Pedal Triangle.

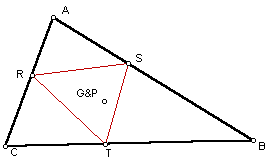
    In this sketch, when the Pedal Point P is the centroid of the given triangle ABC, the Pedal Triangle is completely inside of the original triangle.  This is true for any acute triangle ABC, but when the given triangle ABC is obtuse the Pedal Triangle's location has changed.  In this next example, we will look at an obtuse triangle ABC and what happens to the Pedal Triangle.

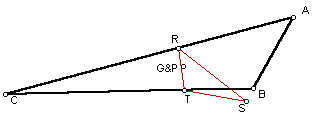
    In this sketch, we can see that the Pedal Triangle RST is not completely inside of the given triangle.  Part of the Pedal Triangle is inside of the given and part is outside of the given triangle.  Next let's see what happens when the given triangle is a right triangle.

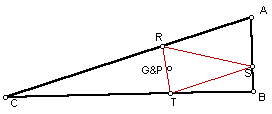
    In this sketch, when triangle ABC is a right triangle, we can see that the Pedal Triangle is still completely inside of the given triangle.  Therefore, we can make the conjecture that when the Pedal Point P is the centroid of the given triangle there are two different types of cases.  When the given triangle is acute or right, the Pedal Triangle is completely inside of the given triangle.  When the given triangle is obtuse, the Pedal Triangle will be part inside of the given triangle and part outside the triangle.

    In this set of drawings, we will look at what happens when the Pedal Point is the incenter of the original triangle.  The first sketch is of an acute triangle ABC.

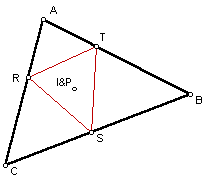
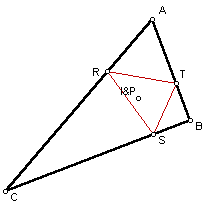
    In this drawing, the Pedal Triangle is completely inside of the given triangle ABC.  In the next two drawings, we will look at an example where the given triangle is a right triangle and an obtuse triangle.

   As you can see from the two drawings, the Pedal Triangle still remains inside of the original triangle in both cases.  Therefore, we can make the conjecture that the Pedal Triangle will always remain inside of the given triangle for any case when the Pedal Point P is the incenter of the original triangle.

   In this set of drawings, we will look at what happens when P is the Orthocenter of triangle ABC.  In the first drawing, we will look at the example where the orthocenter is inside of the given triangle ABC.

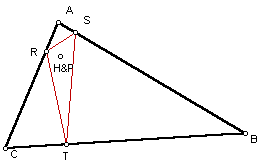
     In this example, when the orthocenter is inside of triangle ABC the Pedal Triangle is inside of the given triangle, as well.  In the case where the orthocenter is inside of the triangle, the triangle is an acute triangle.  In the next example, we will look at the case where the orthocenter is outside of the given triangle.

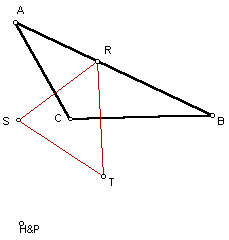
   In this sketch, the orthocenter is located outside of the triangle ABC.  This is always true when the given triangle is obtuse.  Therefore, the Pedal Point P, which is the orthocenter, is located outside of the given triangle.  This effects the placement of the Pedal Triangle.  As you can see from the drawing, the Pedal Triangle is located partly inside of the given triangle and partly outside of the given triangle.  Therefore, we can conclude that when the orthocenter is located inside of the given triangle the Pedal Triangle will be as well.  When the orthocenter is located outside of the given triangle, the Pedal Triangle will be located part inside and part outside the given triangle.

    In the last set of drawings, we will look at the case where the Pedal Point is the Circumcenter of the given triangle ABC.  The first drawing is an example where the Circumcenter is located inside of the given triangle.

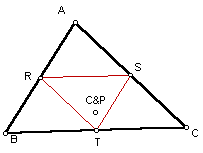
    In this sketch, the Pedal Triangle is located completely inside of the given triangle ABC.  We also know that this triangle an acute triangle because the circumcenter is located inside of the triangle.  In the next drawing,we will look at the case where the circumcenter is located outside of the given triangle ABC.

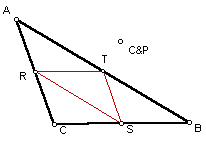
    In this example, when the circumcenter and P are located outside of the given triangle, the Pedal Triangle is still completely inside of the given triangle.  Therefore, we can make the conjecture that the Pedal Triangle will always be located inside of the given triangle if the Pedal Point is the Circumcenter of the given triangle.

    We have looked at many different examples of Pedal Triangles using arbitrary points and specific placements for the Pedal Point P.  In each drawing, we have seen that the movement of P does effect the location of the Pedal Triangle.  In some cases, the Pedal Triangle was completely inside of the given triangle.  In other cases, the Pedal Triangle was completely outside of the given triangle.  In the third type of drawing we have seen, the Pedal Triangle is located in part inside of the given triangle and in part outside of the given triangle.  There are many other cases that you could try and see what happens to the Pedal Triangle, but from what we have seen here the placement of P greatly effects the location of the Pedal Triangle.

Return