Conjecture: Given a triangle ABC with circumcircle of radius R,

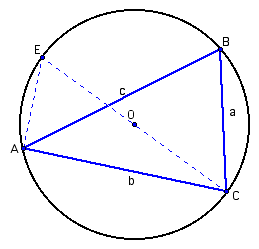
Proof:

We begin by constructing auxiliary diameter CE and auxiliary chord AE. Since angles E and B intercept the same arc, they are congruent and sinE=sinB. Note also that angle EAC is a right angle (angles inscribed in a semicircle are right angles). If we let OC = R, then OE = R and CE = 2R, and

.

Either the results of proof #1 or similar reasoning with angles A and C can be used to complete the derivation of the equation in the conjecture.

Are we finished? Not quite. Once again, our diagram only covers the cases when triangle ABC is acute. What happens when triangle ABC is obtuse?

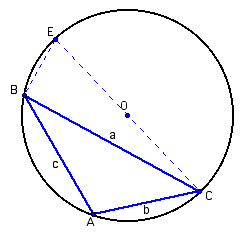
The justification is very similar. Using the diagram above. Note that angles A and E are supplementary (opposite angles of inscribed quadrilaterals are supplementary). Thus,

,

and so on...