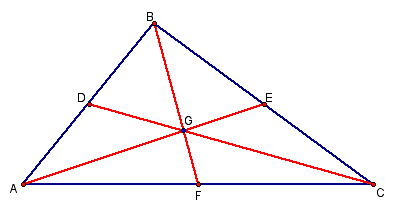
Prove: The medians of a triangle are concurrent.
Click here for a GSP 4.0 sketch to manipulate.

Given triangle ABC, show that medians AE, BF and CD are concurrent.
Since F is the midpoint of AC, AF = FC and
Similarly,
Thus,
By the converse of Ceva's theorem, medians AE, BF and CD are concurrent. The point where these medians intersect is known as the centroid.
Click
here to see a related discussion of medians/centroids on this
site.
Click
here to return to the previous page.