Exploring the Relationships
of
Centroids, Orthocenters, Circumcenters, and Incenters
Now that we've located the centroid
(G), orthocenter (H), circumcenter (C), and incenter (I), let's
explore the relationships among them
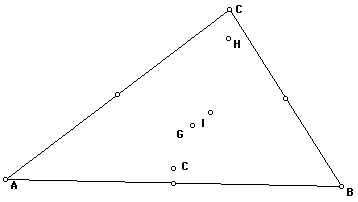 First let's construct a line segment
between points H and C
First let's construct a line segment
between points H and C
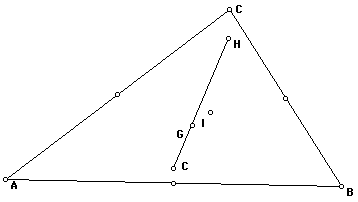 Here we notice that point G is a point
on segment HC
Here we notice that point G is a point
on segment HC
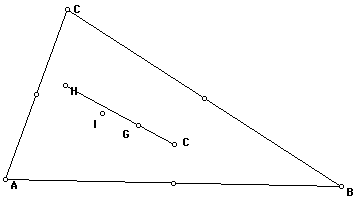 When changing the shape of the triangle
we notice that point G stayed in the center of the triangle and
is still a point
on line segment HC
When changing the shape of the triangle
we notice that point G stayed in the center of the triangle and
is still a point
on line segment HC
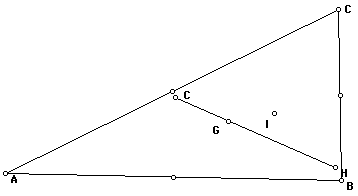 Again changing the shape of triangle
ABC we notice that the circumcenter tends to move toward the midpoint
of the side, where the orthocenter moves toward the vertex
Again changing the shape of triangle
ABC we notice that the circumcenter tends to move toward the midpoint
of the side, where the orthocenter moves toward the vertex
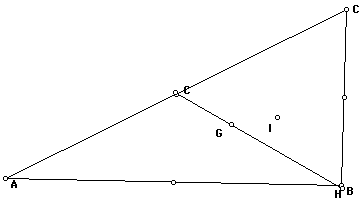 Changing the shape a tad bit more we
notice that the circumcenter does in fact exit the triangle via
the midpoint and the orthocenter via the vertex. All along point
G stayed on segment HC
The following sketches shows that the
circumcenter always exits via the midpoint and the orthocenter
via the vertex
Changing the shape a tad bit more we
notice that the circumcenter does in fact exit the triangle via
the midpoint and the orthocenter via the vertex. All along point
G stayed on segment HC
The following sketches shows that the
circumcenter always exits via the midpoint and the orthocenter
via the vertex
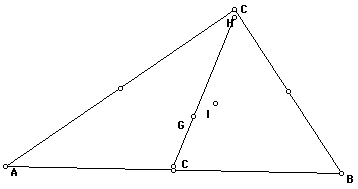
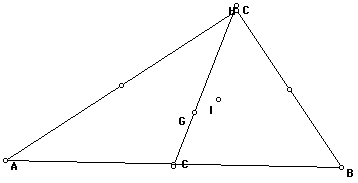
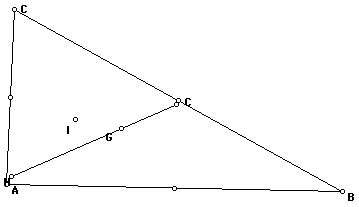
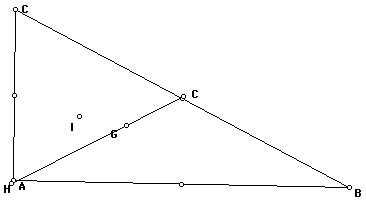 And finally looking at the points throughout
the sketches we can see how the circumcenter looks to always be
equidistant from the vertexes and the incenter looks to always
be equidistant from the sides of the triangle
And finally looking at the points throughout
the sketches we can see how the circumcenter looks to always be
equidistant from the vertexes and the incenter looks to always
be equidistant from the sides of the triangle









