Lastly let's investigate h(x) = f(g(x)) when n = 0
f(x) = -3
g(x) = 5
h(x) = n(nx + 5) - 3, therefore h(x) = -3
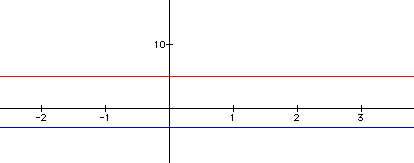
Again we start out with straight lines.
However, what happens when we make n=6
f(x) = 6x - 3
g(x) = 6x + 5
h(x) = 6(6x +5) - 3
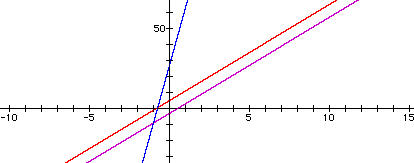
Again we get a straight line.
Let's compare the slopes and y-intercept as we did in the first
investigation
f(x) = 6x - 3
g(x) = 6x + 5
h(x) = 6(6x +5) - 3
h(x) = 36x + 30 - 3
h(x) = 36x + 27
Therefore, the slope is the
product of the slopes of f(x) and g(x) and the y-intercept is
the product of the slope of f(x) and the y-intercept of g(x)
plus the y-intercept of f(x)
Will this stand true when we
set n = 20
f(x) = 20x - 3
g(x) = 20x + 5
h(x) = 20(20x + 5) - 3
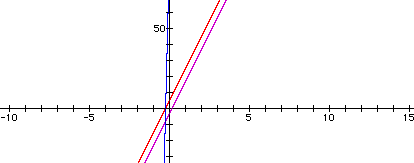
h(x) = 20(20x+5) - 3
h(x) = 400x + 100 - 3
h(x) = 400x + 197
with the slope equal to 400
and the y-intercept equal to 197
Will the composition always
be a linear function? Let's look at the general case
f(x) = ax + b
g(x) = cx + d
h(x) = a(cx + d) + b
h(x) = (ac)x + ad + b
h(x) = (ac)x + (ad +b)
if
s = ac
t = (ad + b)
then we get
h(x) = sx + t
a linear function


