3.3: The Angle Addition Postulate
Now that we have learned how to find a midpoint of a line segment
using Geometry Sketchpadlet's investigate bisecting an angle with
Geometry Sketchpad
Step by Step Instructions
a. Like the construction in the book we start by constructing
an angle
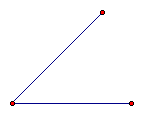 b. Since we are not using a compass, we will select
a point on one of the sides of the angle such that if we construct
a circle with radius equal to the distance from the vertex of
our angle and the new point on our angle, the circle will intersect
both sides of our angle. (Draw point on one side of angle, then
highlight vertex and new point. Select "Circle by Center
& Point" from the "Construction" menu)
b. Since we are not using a compass, we will select
a point on one of the sides of the angle such that if we construct
a circle with radius equal to the distance from the vertex of
our angle and the new point on our angle, the circle will intersect
both sides of our angle. (Draw point on one side of angle, then
highlight vertex and new point. Select "Circle by Center
& Point" from the "Construction" menu)
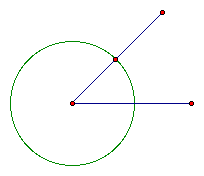
c. Now identify the point where the circle intercepts
the other side of the angle
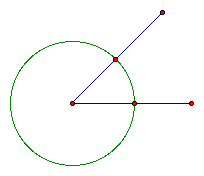 d. Since we want to just focus on the angle let's hide
the circle. (Highlight the circle, from the "Display"
menu select "Hide Circle")
d. Since we want to just focus on the angle let's hide
the circle. (Highlight the circle, from the "Display"
menu select "Hide Circle")
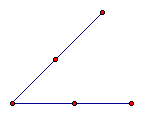 e. To draw the arc in the interior of the angle we
will construct circles from the new points on the angles. Construct
2 circles with the centers being the new points on the angle and
the point on the circles being the vertex of the angle. (Highlight
new point on top segment then highlight vertex, from the "Construct"
menu select "Circle by Center + Point"; do the same
with the new point and vertex on the bottom segment)
e. To draw the arc in the interior of the angle we
will construct circles from the new points on the angles. Construct
2 circles with the centers being the new points on the angle and
the point on the circles being the vertex of the angle. (Highlight
new point on top segment then highlight vertex, from the "Construct"
menu select "Circle by Center + Point"; do the same
with the new point and vertex on the bottom segment)
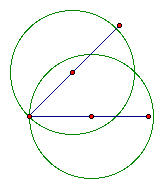 f. Now locate the point where the two circles intercept
in the interior of the angle. Then hide the circles.
f. Now locate the point where the two circles intercept
in the interior of the angle. Then hide the circles.
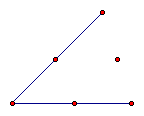 g. Construct a segment from the point in the interior
to the vertex of our angle, this is our angle bisector. (Highlight
point in interior and vertex, from the "Construction"
menu select "Segment")
g. Construct a segment from the point in the interior
to the vertex of our angle, this is our angle bisector. (Highlight
point in interior and vertex, from the "Construction"
menu select "Segment")
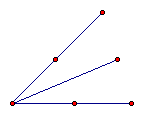 If we had a protractor we could measure the two angles
to see if they were equal, but since we don't let's again use
the "Measure" menu to verify our construction
h. Highlight the endpoint of our original angle, the
vertex, and the point in the interior from the "Measure"
menu select "Angle" do the same highlighting the other
endpoint of our original angle, the vertex, and the point in the
interior.
If we had a protractor we could measure the two angles
to see if they were equal, but since we don't let's again use
the "Measure" menu to verify our construction
h. Highlight the endpoint of our original angle, the
vertex, and the point in the interior from the "Measure"
menu select "Angle" do the same highlighting the other
endpoint of our original angle, the vertex, and the point in the
interior.
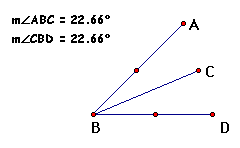
Thus we have verified that our construction is accurate.








