6-1: Medians
Using some of the construction methods used in previous
sections and definitions covered in this section we will explore
Theorem 6-1.
Given the following triangle
Construct the centroid of the triangle then using the measurement
tools show that Theorem 6-1 is accurate.
Step by Step Instruction
We start with the given triangle
 a. First we construct all the medians to locate the
centroid. First we locate the midpoints of the sides of the triangles.
(Highlight the sides of the triangles, from the "Construct"
menu select "Midpoint". Then construct line segments
from each vertex to the midpoint of the opposite line segment)
b. Once you have constructed the medians, locate the
point where the three medians intersect this point is the centroid
a. First we construct all the medians to locate the
centroid. First we locate the midpoints of the sides of the triangles.
(Highlight the sides of the triangles, from the "Construct"
menu select "Midpoint". Then construct line segments
from each vertex to the midpoint of the opposite line segment)
b. Once you have constructed the medians, locate the
point where the three medians intersect this point is the centroid
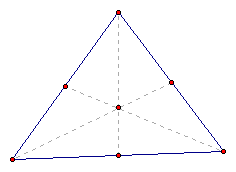 c. Take time to explore that the centroid is actually
concurrent no matter how you change the shape of the triangle.
c. Take time to explore that the centroid is actually
concurrent no matter how you change the shape of the triangle.
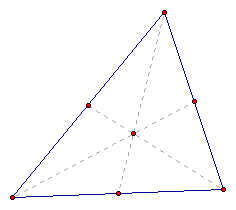
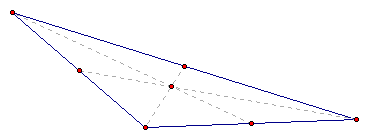
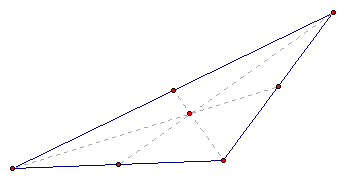 Here we can see that no matter the shape of the triangle
the medians always intersect at one point; therefore the centroid
is always concurrent.
d. Now let's examine whether Theorem 6-1 is true.
Theorem 6-1 states that the length of the segment from
the vertex to the centroid is twice the length of the segment
from the centroid to the midpoint. We can interpret the theorem
in two ways that the distance from the vertex to the centroid
divided by the distance from the centroid to the midpoint is equal
to 2 or the distance from the centroid to the midpoint divided
by the distance from the vertex to the centroid is equal to .50.
We can explore this by using the measure tools.
We will examine our original triangle and the three
previous explorations.
Here we can see that no matter the shape of the triangle
the medians always intersect at one point; therefore the centroid
is always concurrent.
d. Now let's examine whether Theorem 6-1 is true.
Theorem 6-1 states that the length of the segment from
the vertex to the centroid is twice the length of the segment
from the centroid to the midpoint. We can interpret the theorem
in two ways that the distance from the vertex to the centroid
divided by the distance from the centroid to the midpoint is equal
to 2 or the distance from the centroid to the midpoint divided
by the distance from the vertex to the centroid is equal to .50.
We can explore this by using the measure tools.
We will examine our original triangle and the three
previous explorations.
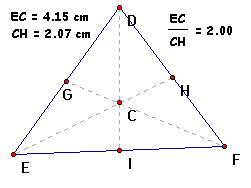
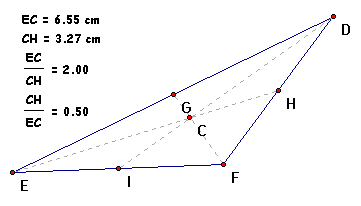
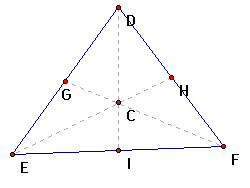 Using the original triange, first we determine the
distance from point E to the centroid. (Highlight point E and
point C, from the "Measure" menu select "Distance".
Then highlight point C and the midpoint of line segment DF, from
the "Measure" menu select "Distance")
Using the original triange, first we determine the
distance from point E to the centroid. (Highlight point E and
point C, from the "Measure" menu select "Distance".
Then highlight point C and the midpoint of line segment DF, from
the "Measure" menu select "Distance")
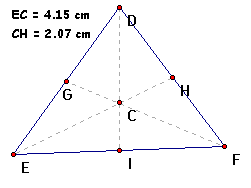 Then we calculate the quotient of measure of line segment
EC divided by measure of line segment CH. (Highlight measures
of each line segment, from the "Measure" menu select
"Calculate". From the "Values" pull down
menu select "m of line segment EC" then select the division
key, then from the "Values" pull down menu again select
"m of line segment CH") We see that the quotient is
equal to 2.
Then we calculate the quotient of measure of line segment
EC divided by measure of line segment CH. (Highlight measures
of each line segment, from the "Measure" menu select
"Calculate". From the "Values" pull down
menu select "m of line segment EC" then select the division
key, then from the "Values" pull down menu again select
"m of line segment CH") We see that the quotient is
equal to 2.
Using the same method calculate the quotient of measure of line
segment CH divided by measure of line segment EC. Here we see
that the quotient is equal to .50.
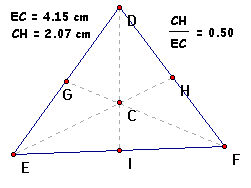
Thus we have verified Theorem 6.1.
Do the same with the previous explored triangles to
see if the Theorem is consistent with them as well
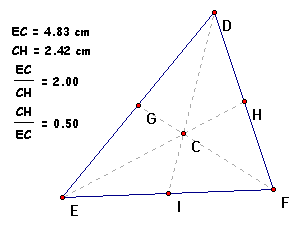
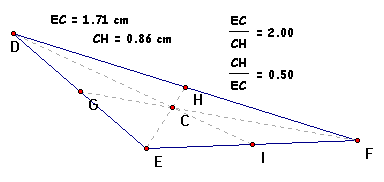
 Yes, we have verified that Theorem 6-1 is true
Yes, we have verified that Theorem 6-1 is true













