11-3: Arcs and Chords
Using some of the construction methods used in previous
sections and definitions covered we will find the center of a
given circle then explore why the construction always works.
A man want's to erect a pole in the center of his circle.
But how does he find that center?

Locate the center using the following method:
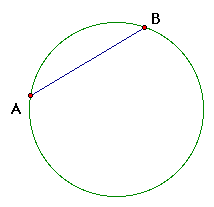
Draw a circle. Within in this circle draw any straight
line AB with point A and B lying on the circle. Now bisect line
AB at point D. Then draw a straight line DC with point C lying
on the circle such that the intersection of the two lines form
right angles. Okay, draw segment AC; bisect AC with a perpendicular
line and you get the center of your circle.
Step by Step Instruction
We start with the given triangle
 Following the construction method each step should
look similar to the following:
a. Construct a segment AB such that points A and B
lie on the circle
Following the construction method each step should
look similar to the following:
a. Construct a segment AB such that points A and B
lie on the circle
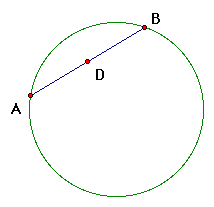
 b. Bisect chord AB at point D (which is the same as
finding the midpoint of chord AB and labeling it point D)
b. Bisect chord AB at point D (which is the same as
finding the midpoint of chord AB and labeling it point D)
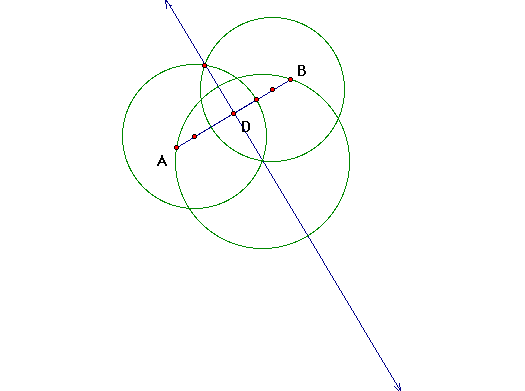
c. Draw a straight line DC with point C lying on the circle such
that the intersection of the two lines form right angles
 Looking at the construction you should realize that
segment DC is a perpendicular bisector
d. Draw segment AC.
Looking at the construction you should realize that
segment DC is a perpendicular bisector
d. Draw segment AC.
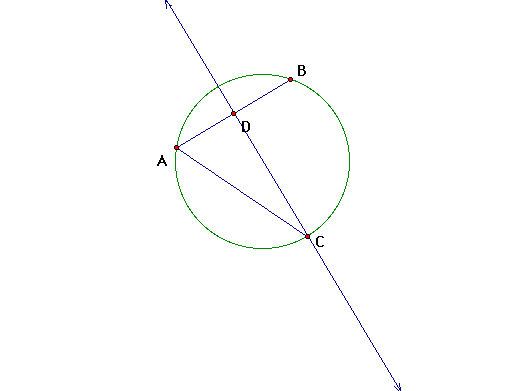
e. Bisect AC with a perpendicular line
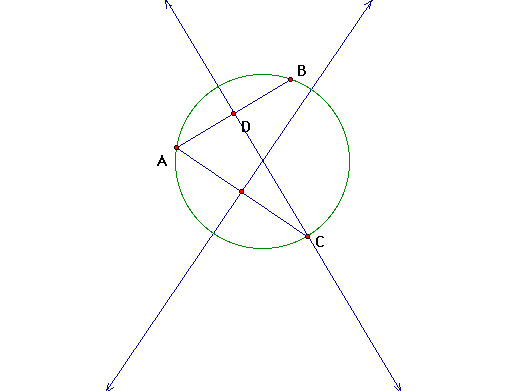
Now we have our center. Identify the center and explain why this
worked?
Explore this with several other different constructions
to verify that this is an accurate construction method
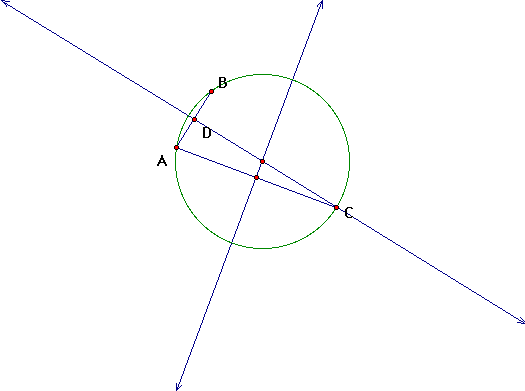
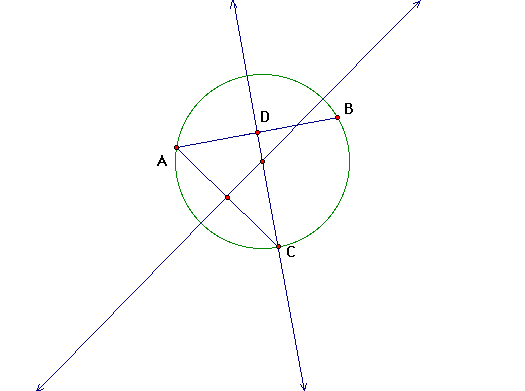
It appears that this construction method will always locate the
center of our circle because of Theorem 11-5 which states:
In a circle, a diameter bisects a chord and its arc if and only
if it is perpendicular to the chord.









